[Gas Dynamics] Ch 8 Prandtl-Meyer Flow - Application - Airfoil

 

 

Prantl-Meyer flow 마지막 Post입니다.

정말 여기서 끝낼께요

 

지금 실제 Oblique shock, Prandtl-Meyer flow가 

언제 어디에서 어떻게 발생하는지 보고있고,

이전 포스터에서 1.Nozzle

이번포스터에서 남은 2.Wave reflection, 3. Airfoil 끝내겠습니다

 

 

2. Wave Reflection

 

예제 문제로 보면서 이해해 봅시다

 

Given:

Flow of Air

M1 = 2.2

θ1 = 35도

 

Q. beta?, Two shocks strength increase or decrease?

 

 

 

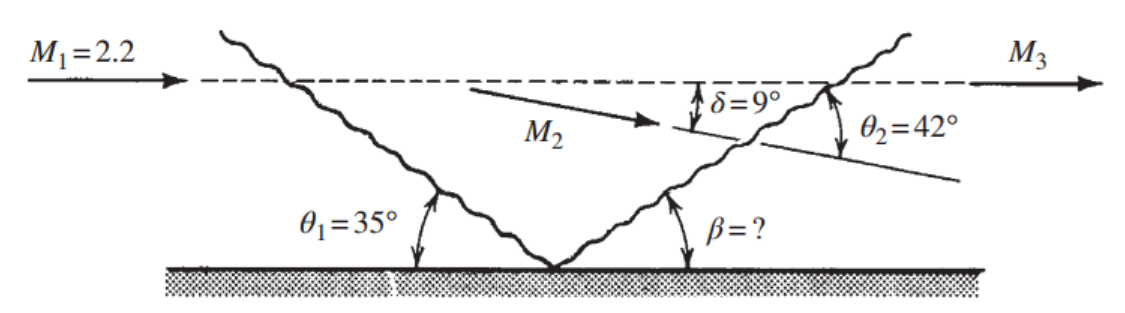
즉 Wave는 바닥면에 의해 Reflect 될수 있지만,

Shock Strength 는 감소 함을 알 수 있다.

 

 

3. Airfoil

 

 

마지막 Application 빠르게 살펴보고

Ch 8 종료 해봅시다.

 

 

 

Airfoil특징은 Sharp한 Edge가 무조건 있다는 것이다.

 

Moreover,

 Angle of attack(유체와 비행기의 각도) > 0 인 경우가  발생한다.

이런 경우 Pradntl Expansion Wave가 무조건 생긴다.

 

 

Region 1 -> 2

Sharp한 Edge에 유체의 방향 꺽여야 하므로

Pradntl Expansion Wave

P1 > P2 압력감소

 

Region 1 -> 3

Sharp한 Edge에 이번에는 벽면을 올라가는 식으로 꺽이므로

Oblique shock

P1 < P3 압력 증가

 

'P3 > P2 이므로

압력차이로 Airfoil 위로 올리는 Lift force 발생'

 

 

※ 급 질문.

Q. 왜? Prandtl Compression wave 아닐까?

Compression wave 는 Round한 연속적으로

deflection angle이 변하는 경우만 발생.

 

 

 

 

이후 Boudary condition 2가지를 만족 시켜야 한다.

1.V4 // V5

2. P4 = P5

 

이를 위해서는,

비교적 낮은 압력 P2는 압력을 상승 해야하고,

Reversly, 높은 압력 P3는 압력을 감소 해야함.

 

Therefore,

 

Region 2 -> 4

Oblique shock을 발생시켜

P2 < P4 압력 증가

 

Region 3 -> 5

Prandtl Expansion wave 발생

P3 > P5 압력 감소

 

이렇게 최종적으로 영역 4,5에서

속도의 방향이 같고, 압력이 같은 유체가 형성된다.

 

 

[마지막 예제 문제를 풀어보고 마무리 하겠습니다.]

 

 

 

 

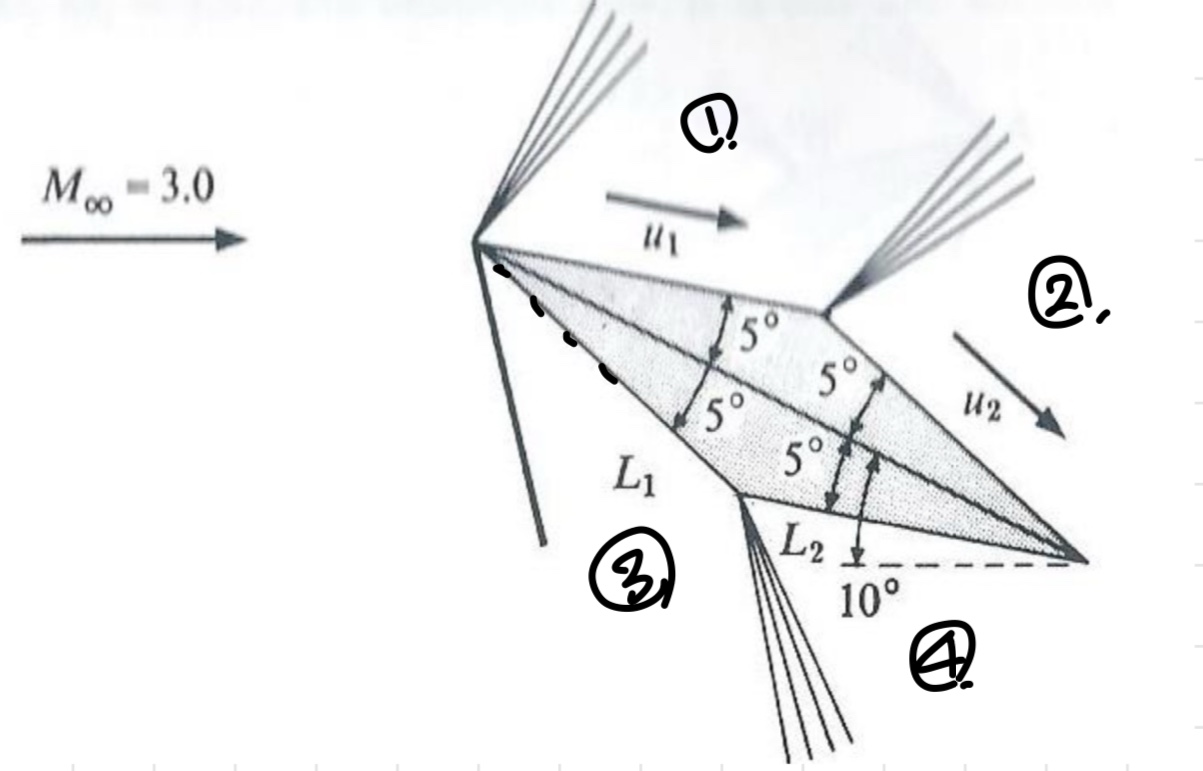
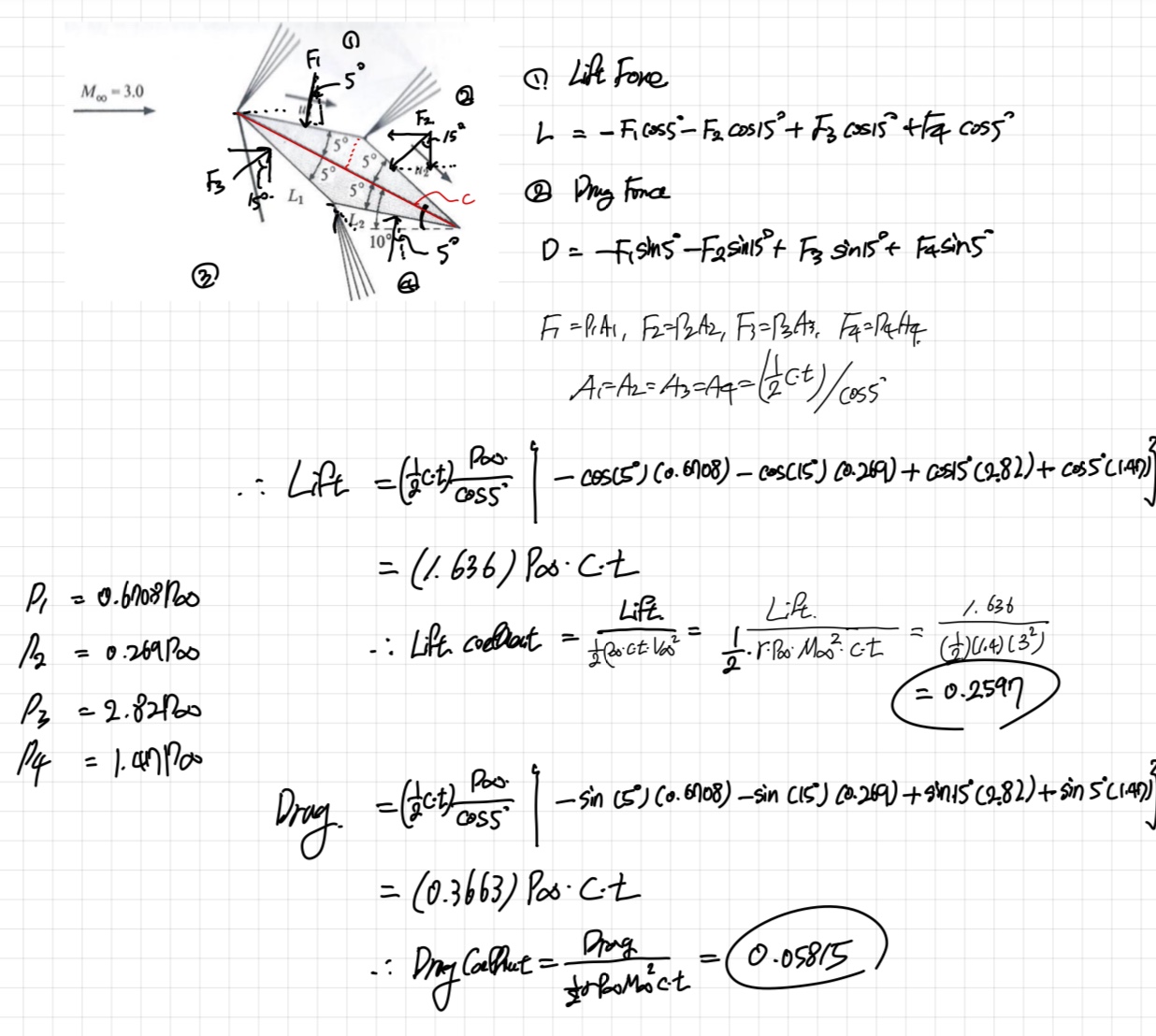
Q. For the 2-D airfoil shown above Fig,

Compute the Lift and Drag coefficients for an angle of attack of 10 degrees.

 

 

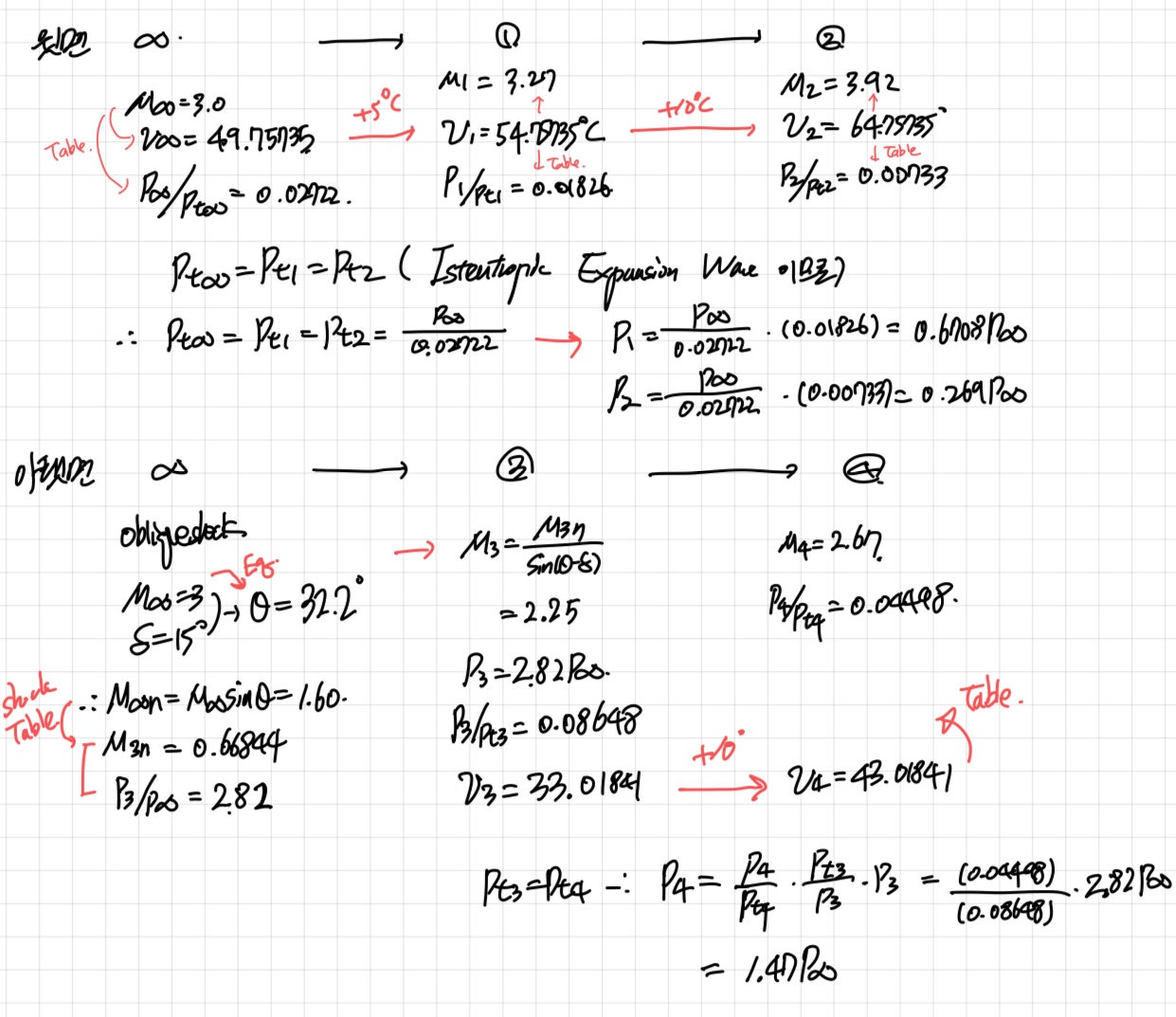
면적항을 위해 폭을 t라고 하자.