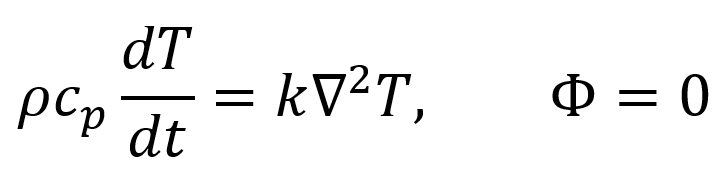[Fluid Mechanics] Ch 4. Differential Relations for fluid flow - Linear momentum

지난시간 유체역학에서 가장 중요한 식

Navier's stokes equation을

증명해보았습니다.

 

이번에는 마지막으로

Differential relations for fluid flow

3. Energy Equation을

증명해보겠습니다.

 

먼저 Reynolds transport Theorem Energy eq에서

 

work term = shaft work + viscous work + pressure work 으로

나눌 수 있고, Pressure work를 우항으로 넘겨 

Flux term과 합쳐줄 수 있었습니다.

[자세한 증명 아래 내용참고]

https://jeffdissel.tistory.com/4

[Gas dynamics] Ch 2 - Control volume analysis - Application of Reynolds Transport Theorem

 

이 적분식을 

 

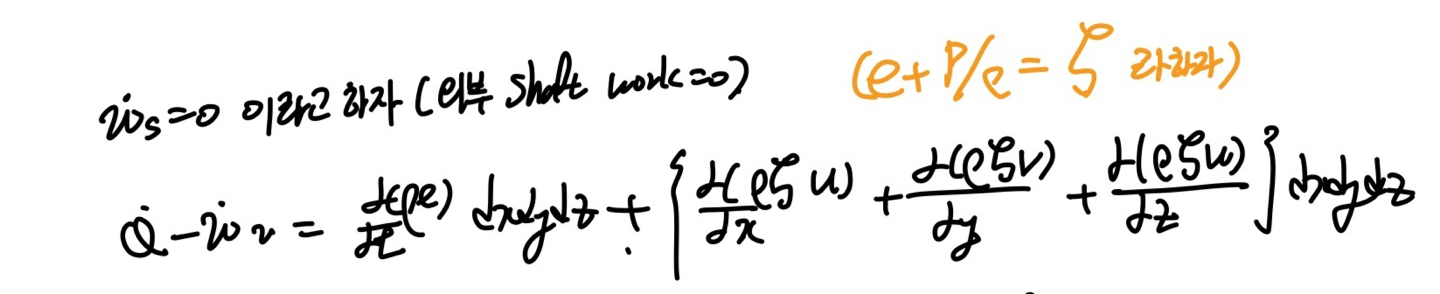
위 식과 같이 미분 형태로 나타낼 수 있다.

 

 

단위부피당 열과 일, q,w로 나타낸후, 미분식을 풀어주면,

 

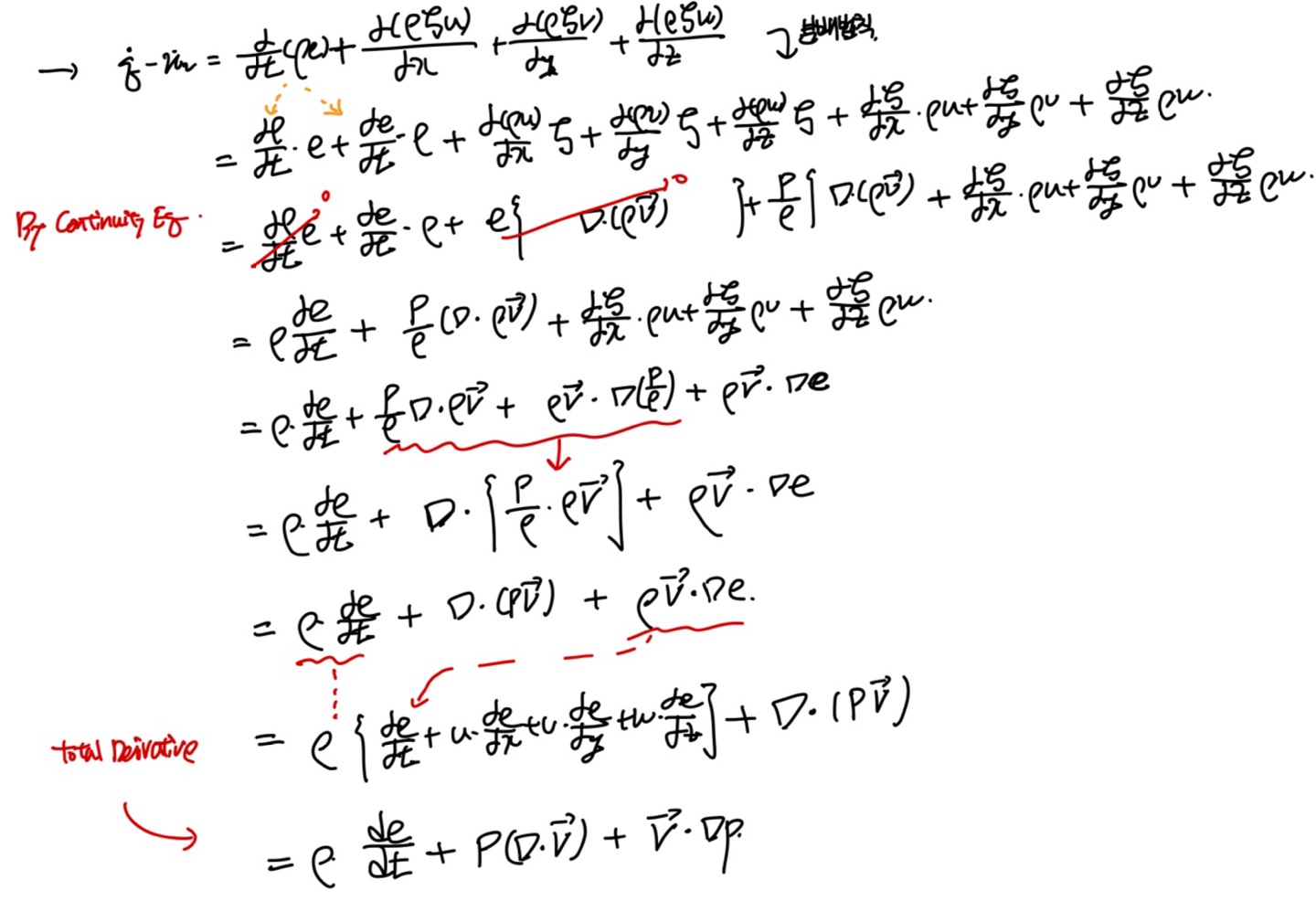
3개의 term으로 이루어진 식이 유도된다.

 

 

 

 

지금까지 우항 term을 식으로 풀었고,

이제 좌항의 단위부피당 열과 viscous work term을 식으로 유도해보자.

 

먼저 이렇게 작은 dx,dy,dz control volume이 있다고 가정하자.

 

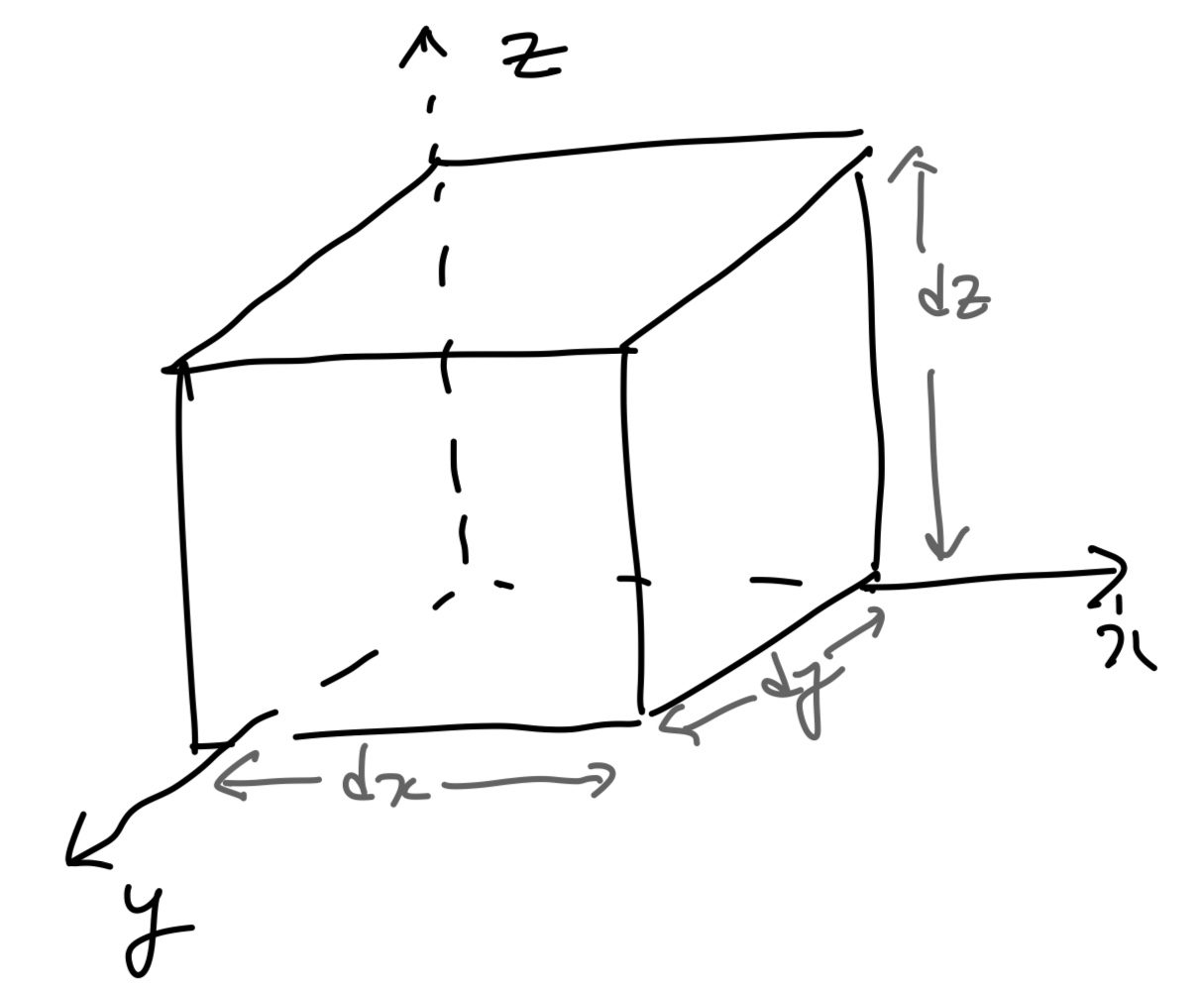
이제 들어오고 나가는 열량, 그리고 shear workterm을 계산해주면

 

 

 

 

 

구한후, 원래 구했던 우항 식들과 같이 연결 시켜준다.

 

e를 분리해주고 정리해주면, 아주 신기하게 Linear momentum eq이 나와서 0 이 되버린다.

 

최종 Energy equation derive 완료...

 

 

 

 

당연히 몇가지 가정을 하게되면 Simplify 가능

 

 

1. Cv, ρ, viscosity(u), k 가 일정할때

 

incompressible flow 이므로, 밀도가 일정하고, continuity eq에 의해

 

∇·V = 0

 

그리고 Cv는 일정하므로, du = Cv dT 로 바꿀 수 있다. 따라서,

 

 

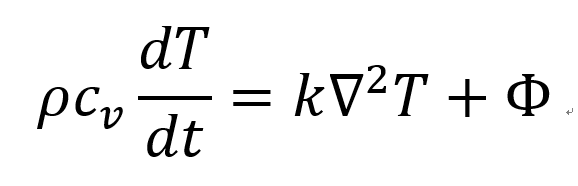
2. 유체가 정지해 있을때

 

정지해 있는 경우, pressure constant 이므로, Cv = Cp로 전환 할 수 있고, 속도 = 0 이므로,

Viscous dissipation rate = 0 으로 전환된다.