이제 heat conduction 문제를
지금까지 배운 이론들을 가지고 풀어보자.
Steady 1D Heat conduction w/ Source term를 가지고 연습을 진행해보자.

위 식을 ch3에서 배운 Method of Weight Residual방식으로
적분함수로 바꾸면 다음과 같다.
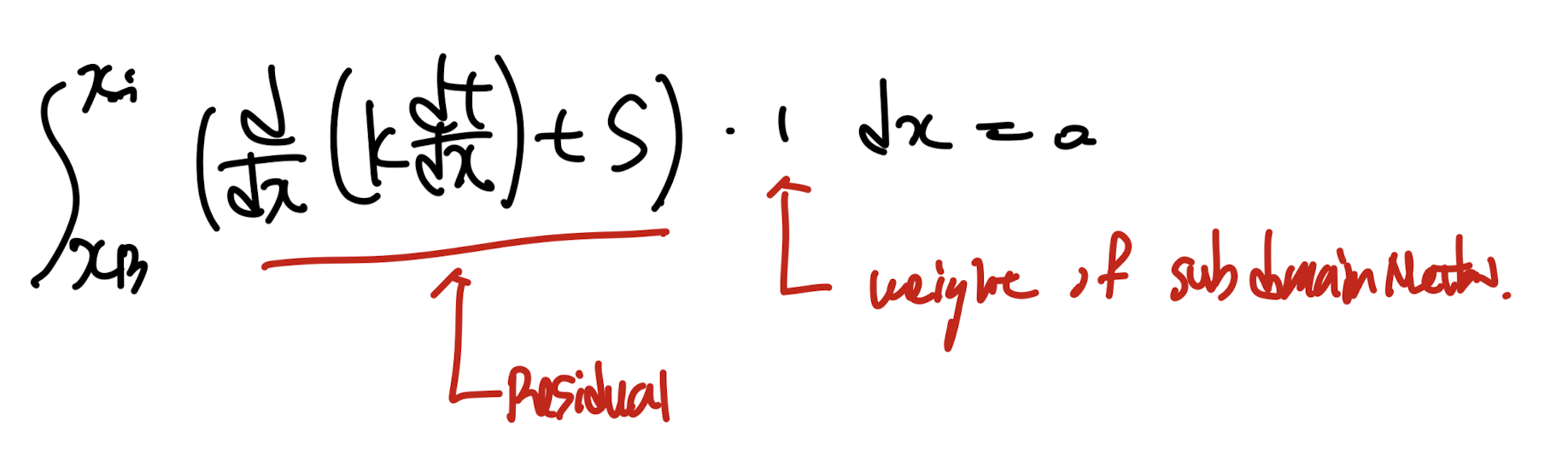
위 문제를 discretization equation으로 바꾸는게 우리의 목표이지만,
바꾸는 과정에서 몇가지 짚고 넘어가야할 부분들을 체크하자.
1. Harmoninc Mean
여기서 control volume으로 domain을 쪼개고 위 식을 각 cv마다 적용하려면,
사이 interface에서 heat conductivity k_e가 요규된다.
하지만 만약에 P,E가 서로다른 material domain이라,
x=e를 기준으로 material이 바꾼다면??

ke = kP? KE?
우리는 ke를 특정 규칙에 따라 정의해주어야 한다.
첫번째 방법은 그냥 interpolation즉 P,E로의 거리비율을 이용하여,
ke를 정의하고 'Arithmetic Mean'이라고 칭한다.
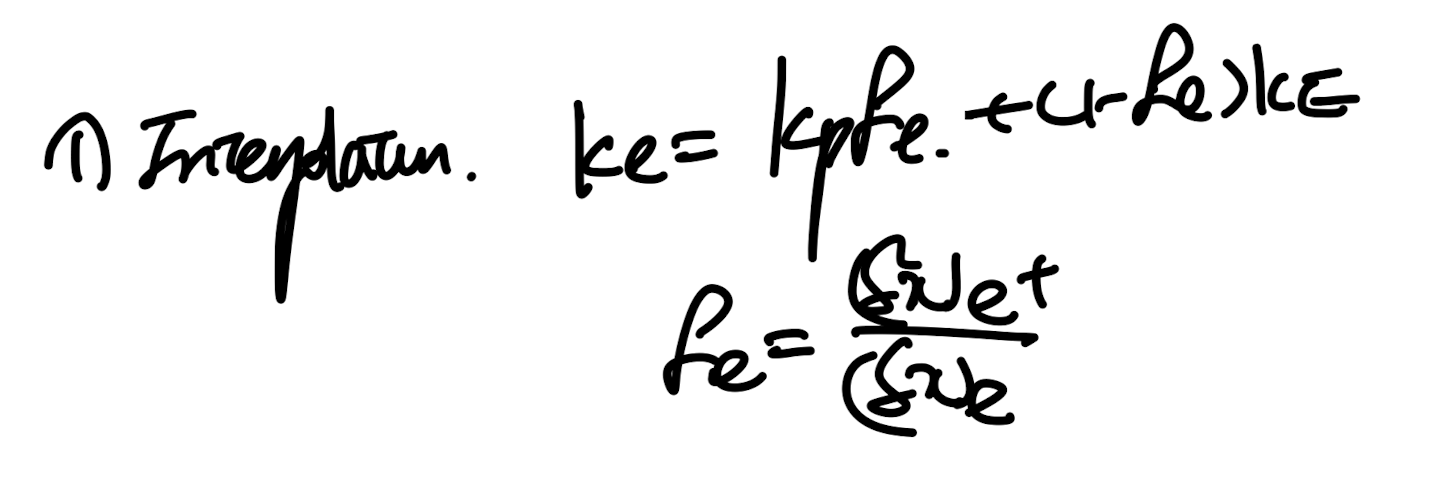
두번째 방법은 Harmonic Mean즉 열전달 시간에 배웠던,
Thermal resistance, Current 개념을 사용하여 계산하는 것이다.
물질은 다르더라도 Heat flux(current)는 동일하다는 점을 이용한다.
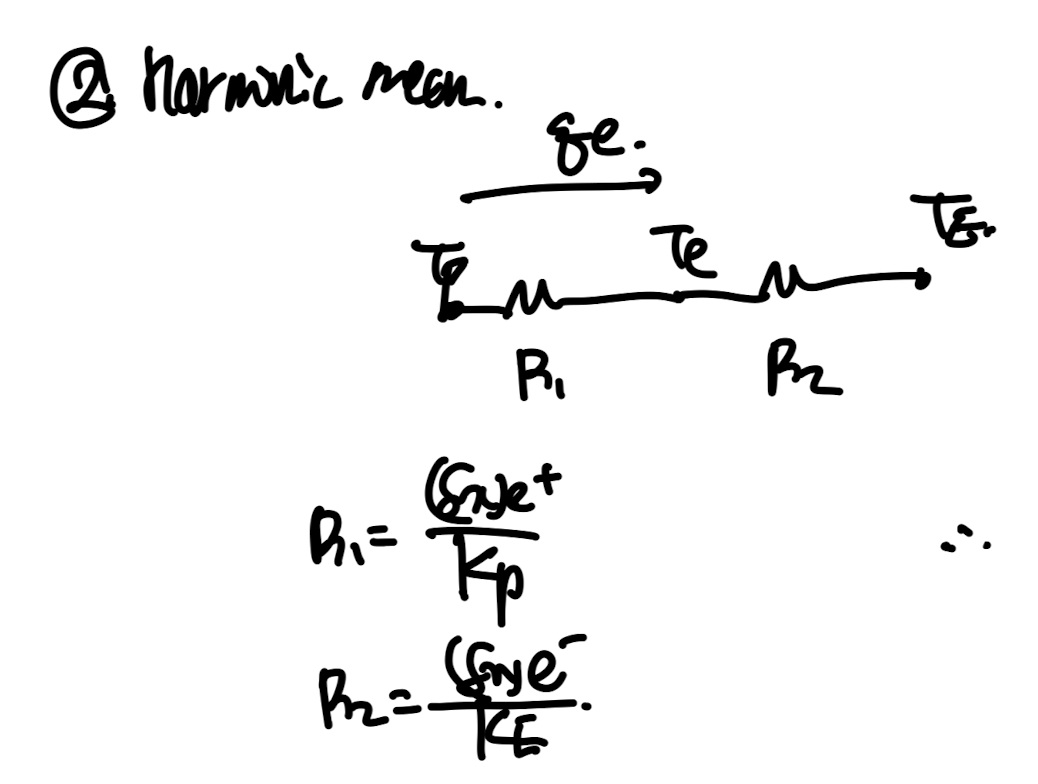
위 diagram처럼 각 thermal resistance를 구할 수 있고,
이를 Total Thermal resistance dx_e/ k_e로 정의하여 다음과 같이 식을 유도가능하다.
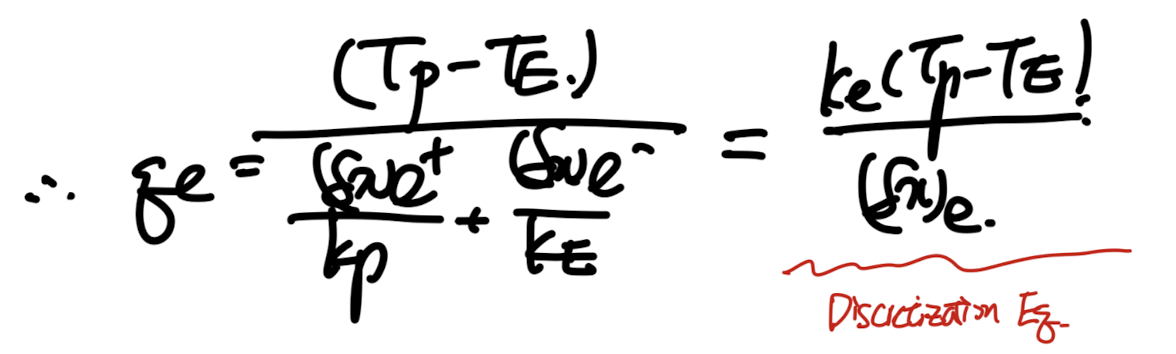
만약에 grid 간격이 일정한 상황(center node on the CV)이라면,
우리는 다음과 같이 ke를 Kp,KE의 함수로 유도가능하다.
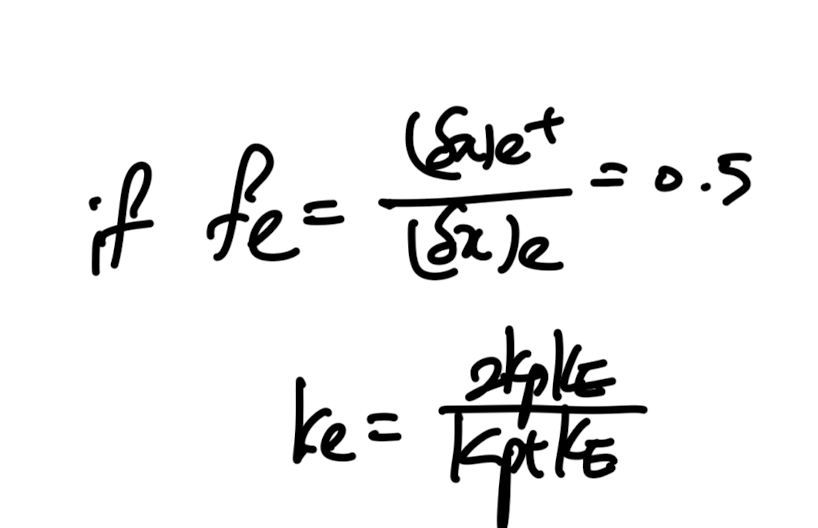
자 위에서 정의한 두 방식중 어느 방식이 더 물리적으로 타당한지를
한번 살펴보자.
1. 단열 boundary condition의 경우
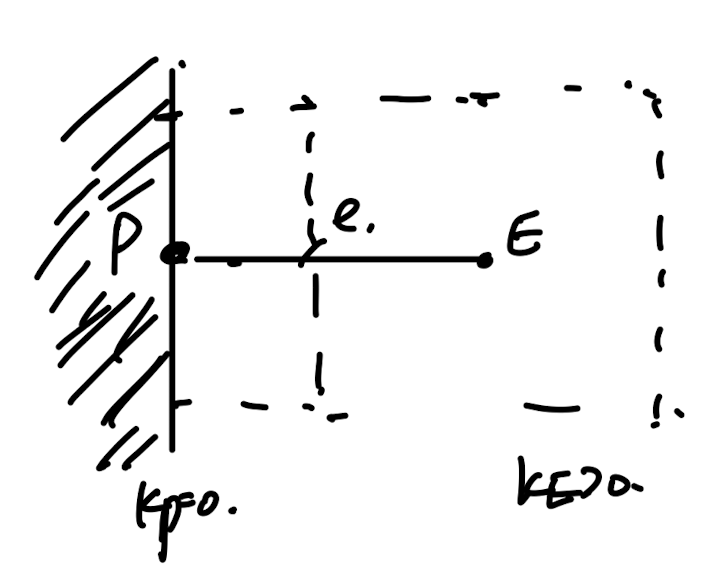
즉, k_p -> 0 인 경우이다.
각 Arithmatic, Harmonic mean을 살펴보면, Arithmetic인 경우 qe > 0 이라는 모순이 나오게 된다.

결론적으로 Harmonic Mean 이 Insulated BC에서 더 물리적으로 타당하다.
2. Abrupt Material property variation(Kp>>KE)
열전달 시간에 분명히 다루었을 문제이다.
만약에 K값이 급격히 변하면 Temperature gradient(T-x graph 기울기)가 급격하게 바뀐다.
여기서 실제로 KP가 너무 크기때문에 TP ~= Te임을 이용하여,
heat flux를 다음과 같이 e-E영역에서 P-E영역으로 확장시킬 수 있다.

따라서, total Thermal resistance - dx_e+/KE임을 알 수 있고,
이는 우리가 ke를 이용하여 표현한 heat flux와 동일해야하기 때문에,

Fe = 0.5가정을 하면, ke = 2KE
자 이제 맨처음 정의한 Arithematic, harmonc mean식에
Kp >> KE를 적용하면 다음과 같이 ke가 유도된다.

즉 결론적으로,
ke = 2KE 가 Physically meaning(Heat flux is constant)한 것을 위에서 증명하였고,
이 결과는 Harmonic Mean 가정에서의 ke와 동일함을 알 수 있다.
Therefore,
Harmonic Mean is More physically reasonable for the
'Insulated BC' and 'Interface consistency'
compared to the 'Arithematic Mean'
라고 우리는 결론을 지을 수 있다.
'Numerical Heat transfer and Fluid flow' 카테고리의 다른 글
| Ch4 Heat conduction - part3 (Boundary Conditions, TDMA) (1) | 2025.04.19 |
|---|---|
| Ch4 Heat conduction - part2 (Source term Linearization) (1) | 2025.04.19 |
| Ch3 Discretization method - summary (0) | 2025.04.15 |
| Ch3 Discretization method - part3 (4 Basic rules) (0) | 2025.04.14 |
| Ch3 Discretization method - part2 ( WRM, FVM) (0) | 2025.04.14 |




