Fluid dynamics에서 Flow종류를 다양한 기준을 통해서 category를 분류한다.
그 중에서 Reynolds number가 큰 flow를 우리는 Turbulence flow라고 부른다.
(이와 반대로 작은 flow를 우리는 Laminar Flow라고 칭함)
'지금 배우고 있는 모든 이론들은 결국 물리적 의미를 단지 수식으로 표현한 것이다'
그렇다면 위 Reynolds number와 Turbulence Flow는 어떠한 물리적 의미를 함축하고 있을까?

여기서 Reynolds number이 작을수록 점성력이 지배적이어서,
유동이 안정적이고 정돈된 Laminar flow가 유지된다.
하지만 Reynolds 수가 임계값을 넘어서면,
관성력이 우세해져 유동이 불안정해지고 난류(turbulence) 상태로 진화하게 된다.
여기서 점성력의 물리적 역할은
'어떠한 속도차이가 나는 두 유체입자의 속도를 맞춰주는 브레이크 역할을 한다'
따라서, 속도차이로 인해 발생하는 현상들을 억제하는 역할을 한다는 것.
위 점성력의 역할과 안정(Laminar)-불안정(Turbulent) 이라는 대비 개념을 가지고,
Boundary layer flow on the flat plate를 밑에 그림에서 살펴보자.

어떠한 판이 바닥에 깔려있고, 그 판위에 오른쪽(+x)방향으로 유체를 불어 넣어준다.
여기서 plate와 유체와의 viscous shear stress(마찰력으로 인한 stress)로 인해서
plate부근에서 유체의 속도는 감소한다. (정확히는 모멘텀이 손실된다)
초기에는 판과의 점성 마찰로 인해 Boundary Layer이 형성되고, 이 속도 구배가 큰 층에서 층류가 유지된다.
따라서, 밑의 velocity profile을 얻게 된다.

그러나 경계층이 발달하면서 유동은 점차 작은 교란들이 증폭되며 transition zone을 거쳐 결국 난류로 넘어간다.
이때 난류는 단순히 “섞이는 유동”이 아니라, 무작위적이고 3차원적인 에너지 전달 구조를 가지며,
시간과 공간적으로 매우 복잡한 움직임을 보이기 때문에 통계학적 수단으로만 예측이 가능하다.

다시 간단한 언어들로 표현하면,
교란들의 발생을 (점성력 >> 관성력 인 경우)는 점성효과로 인해서 억제할 수 있지만(Laminar Flow),
(관성력 >> 점성력인 경우)는 교란을 억제하지 못하여 random motion을 띄게 된다.
그게 바로 Turbulent Flow.
고체의 벽에 의한 점성으로 난류가 발생하는 것(Wall-bounded flow)과,
벽 없이 점성으로 난류가 발생하는 기준(Free shear flow)으로 우리는
flow를 다음과 같이 구분할 수 있다.
Free shear flow
-jet, wakes, shear layer
Wall-bounded flow
- Boundary layer flow, channel flow, pipe flow.
여기서 turbulent flow를 분석하기 위해,
governing equation들을 이번 글에서는 살펴보고
다음 블로그에서는 통계학적 분석을 자세하게 살펴보자.
1. mass conservation -> Continuity Eq.
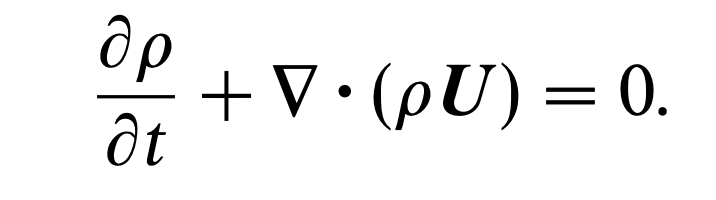
여기서 specific volume이 변하지 않으면(Incompressible Flow),
즉 density가시공간에 따라 일정하다면,
우리는 위 식을 통해 다음 관계식을 얻을 수 있다.
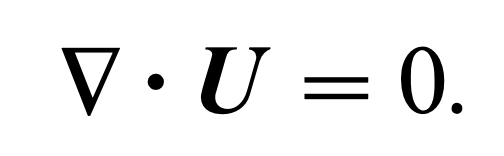
2. Linear Momentum conservation
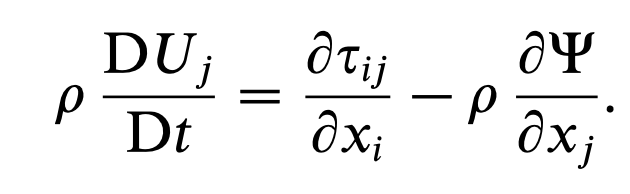
유체역학 시간에, F = ma에서 body, surface force로 분류한 후,
infinitsimal small fluid 에 대해서 우리는 위 모멘텀 보존 식을 유도하였다.
여기서 Newtonian fluid 가정을 한다면, 우리는 shear stress tensor를 다음과같이,
압력 과 strain rate 로 나타낼 수 있다.
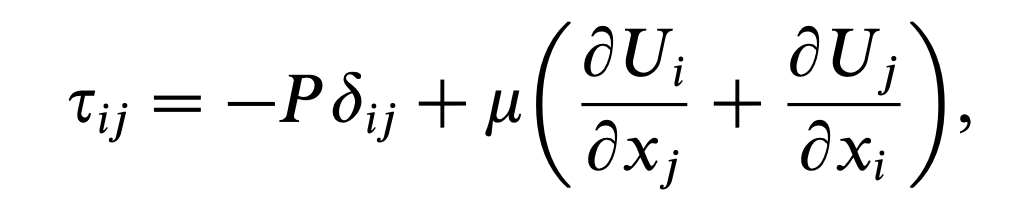
따라서, linear momentum conservation 식에 위 newtonian fluid shear stress를 대입하면,
다음 식이 유도되고, 여기에 Incompressible flow 가정도 추가해주면,
다음의 Navier's Stokes 방정식이 유도된다.

여기서 우리가 압력과 body force potential를 하나의 modified pressure로 정의하면,

simplified NS 방정식이 유도된다.
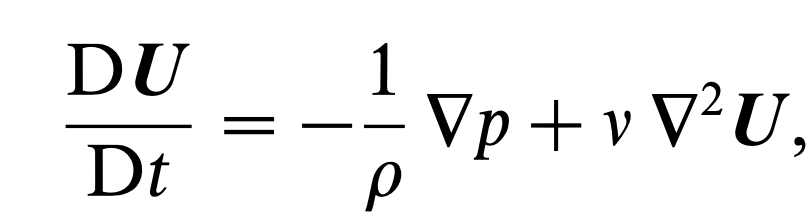
보통 두가지 boundary condition이 가장 많이 쓰이는데,
1. impermeability condition(벽과 수직방향의 속도성분 = 0 )
2. no slip condition(벽과 수평방향의 속도성분 = 0)
따라서, 벽에서의 속도벡터 자체가 0.

No visocus effect -> Inviscid Flow. 의 가정이 추가된 경우 우리는
diffustion term을 날려버려 아래와 같이 두가지 term만 남길 수 있고,
밑의 식을 Euler's Equation이라고 칭한다.

여기서 하나의 식을 더 유도해보자. 먼저 incompressible NS 방정식은 아래와 같다.

그리고 1식을 divergence를 양변에 진행해준다. 연산을 편하게 하기 위해. Index notation을 사용하자.

여기에, continutiy Eq(incompressible)가정을 추가해주면 우리는 4번의 Possion Equation을 도출 할 수 있다.

4번 방정식을 유도한 이유는, 우리가 속도와 압력을 가지고 있을때 이 데이터가
continutiy eq와 linear momentum Eq을 동시에
만족하는지를 알 수 있다는 것이다.
지금까지는 속도장에 관한 식만 살펴보았지만, 이것을 일반화하여, 우리는 Transport Equation으로 확장해보자.
Conserved Passive scalar function Φ(x,t)에 대해서 보존 법칙식은 아래와 같다.

여기서 아무 scalar function이면 안되고,
Conserved: 전체 system의 particle이 가지고 있는 scalar값의 총량은 보존
Passive: 다른 material property, velocity 등등 particle의 다른 값에 영향을 주지 않는다.
두 성질을 지닌 scalar function이어야 한다.
한가지 더 중요한 성질은 boundness이다. scalar함수의 domain(x,t)에 대해서
scalar함수값의 범위는 유한하다는 것이다.
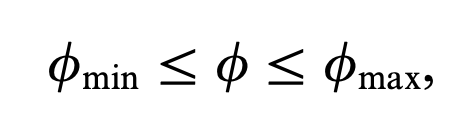
#strain rate tensor

유체역학 시간에 계속해서 나오는 strain rate tensor,
shear stress와 비례하는 항이기 때문에 계속해서 나올 수 밖에 없다.
strain rate tensor를 symmetric, antisymmetric part이렇게 2가지로 나누면, 아래와 같다.
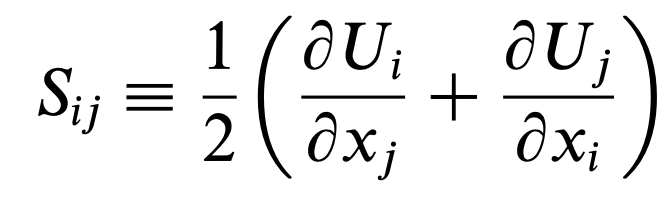

'Fluid Mechanics' 카테고리의 다른 글
| [Turbulent] ch3 - The statistical description of turbulent flows (1) | 2025.05.07 |
|---|---|
| [Fluid mechanics] Reynolds Stress (0) | 2024.05.13 |
| [Fluid mechanics] Stress tensor_Lame's Parameters part2 (0) | 2024.05.13 |
| [Fluid mechanics] Strain tensor (0) | 2024.05.13 |
| [Fluid mechanics] Stress tensor_Lame's Parameters (0) | 2024.05.13 |



