지금 우리가 뭐하고 있는지 다시 짚어 보자.
Ch5 에서 Area가 Change 하는 경우
Continuity Equation, Ideal gas flow 로부터
밑의 식을 유도 했었다.
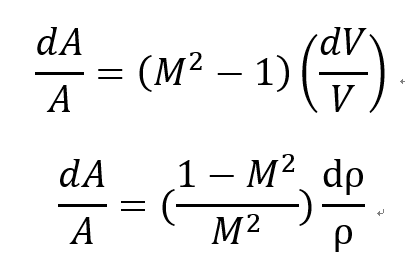
dA/A를 substitute 해주면,
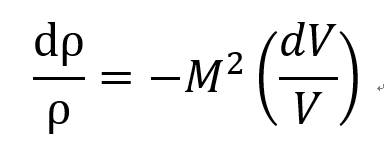
위 식이 의미하는 바는 마하수 M이 클수록
밀도 변화가 속도 변화에 주는 영향이 커진 다는 것이다.
유체역학 시간에
배웠던 거의 모든 Flow들은
Incompressible flow
즉, 밀도변화를 무시할 수 있는 유체의 흐름이 었다.
However, Gas Dynamics에서 우리는 Compressible flow
밀도 변화가 있는 경우 유체의 흐름을 분석하고있다.
그리고 Compressible Flow에서 가장 중요한 3가지 Factor에 대해서
Ch5에서 언급하였다
1. Area change
2. Friction
3. Heat transfer
So far, 우리는 Area change 하는 경우의 Flow
+ Shock
+Expansion wave
에 대해서 알아보았다.
이제는 2번째 Factor Friction 이 있는 경우 를 해석해보자
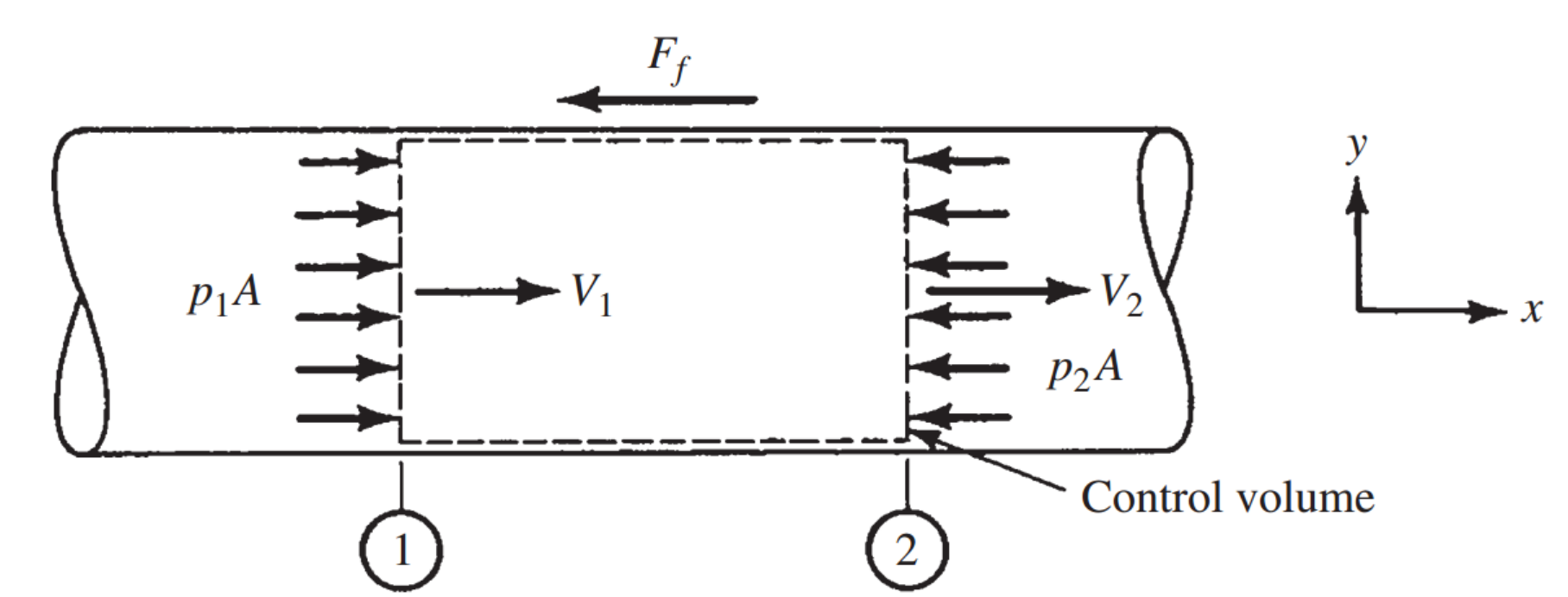
위 사진과 같이 C.V을 설정해주고 다음과 같은 가정을 해주자..
#Assumptions
1. .Steady 1-D flow
2. Adiabatic
3. No shaft work
4. Neglect potential
5. Constant Area
6. Friction Exists
이제 뭘 해야할지 느낌이 오실 것이다.
1. Continuity Eq, 2.Momenum Eq, 3. Energy Eq.
연속방정식, 에너지 보존식을 먼저 살펴보면

면적이 같으므로 ρV 는 일정하다 따라서
우리는 G라고 정의하고 Mass velocity로 부르자
Stagnation Enthalp도 일정할 것이다.(No heat transfer and shaft work)
따라서 Neglect potential 이므로 E equation을Mass velocity(G)와 ρ로 표현해보자

위 식을 그래프로 한번 그려보자.
ht 는 일정하기 때문에
G가 일정한 경우 -> h, 1/ ρ 반비례

위 사진을 보면 G가 일정한경우의 h-v Line을 Fanno Line 이라고 부른다.
뿐만아니라 위 그래프에서 엔트로피 Line(점선)을 보면
Fanno Line은 v가 증가할때
엔트로피 증가 -> 최대 -> 감소
임을 눈으로 확인 할 수 있다.
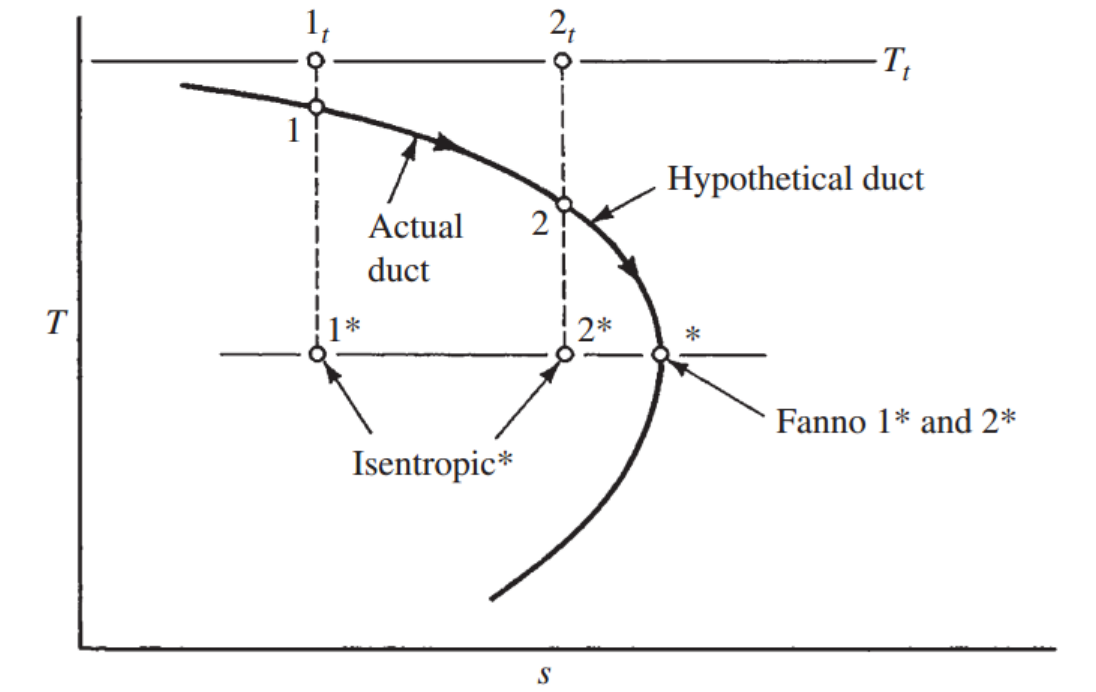
Fanno line에서 엔트로피 변화를 보기 위해 h-s그래프로 옮겨보자
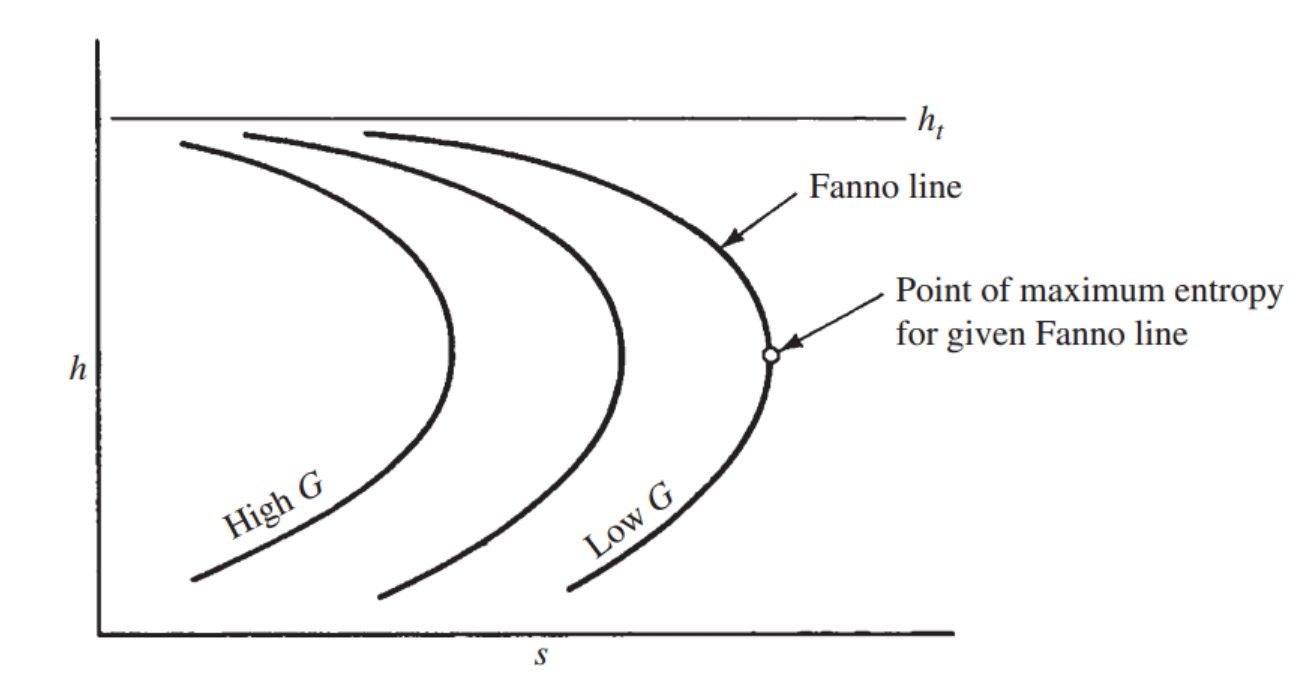
위 그래프를 통해서 우리는
각 Fanno line마다 엔트로피가 Max인 지점이 있다는 것을 확인 할 수 있다.
그 지점이 무엇이고 의미하는게 뭘까??
먼저 위에서의 continutiy eq 과 Energy eq을 각각 미분해주자.
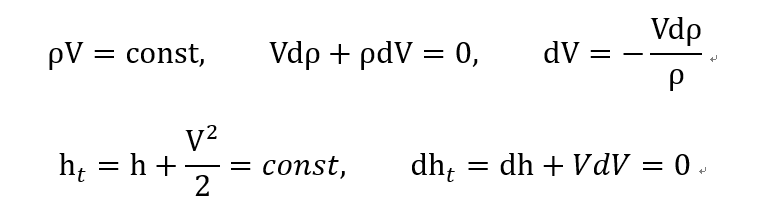
위 dV 를 밑에 대입해주면
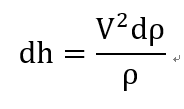
여기서 ds = 0 지점을 우리는 분석하려고 하므로,
Energy equation 을 통해서

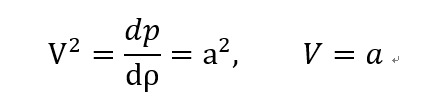
위에서 구한 dh를 대입해주면 최종적으로 ds = 0 일때,
s max 일때, 우리는 Ma = 1 임을 알 수 있다.
그렇다면 우리는 엔트로피 증가법칙!이 떠오를 것이다.
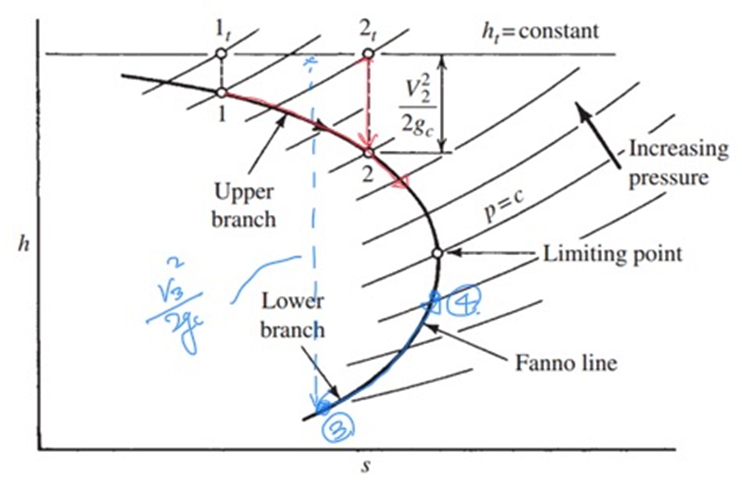
따라서,
Upper branch: State 1 -> 2 -> Limiting point
Subsonic -> high subsonic -> sonic
Lower branch: State 3 -> 4 -> Limiting point
Supersonic -> low supersonic -> sonic
아주 신기하게 마찰이 있는데 subsonic은
속도가 증가하여 Ma =1, sonic flow가 된다는것;;;
조금 더 식을 통해서 정확히
Property들을 표현해보자.
이제 1->2 과정에서 온도, 압력 , 정적압력 변화를 살펴보자.

먼저 온도 비율은 Stagnation enthalpy 를 통해

다음 압력비율은 연속방정식으로

마지막으로 Stagnation Enthalpy는
Tds = dh - vdp, p= ρRT 식 적분을 통해

따라서 Stagnation pressure- entropy equation 에 대입해주면

마지막으로 the most important 할일이 하나 남았다.
Momentum eq을 통해 마찰력을 계산하는것 !!

가정 1->2 길이 = dx
why? dx에 관한 마찰식 밑에 알고 있으니
나중에 적분할려고
[혹시 모르시면 밑에 링크 참고!]
https://jeffdissel.tistory.com/7
[ch3 에서 증명한 friction flow momentum + energy equation]
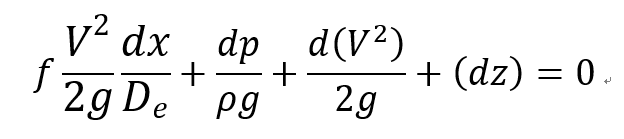
여기서 potential term 을 무시하고 V= M*a, p = ρRT 를 대입해주자.
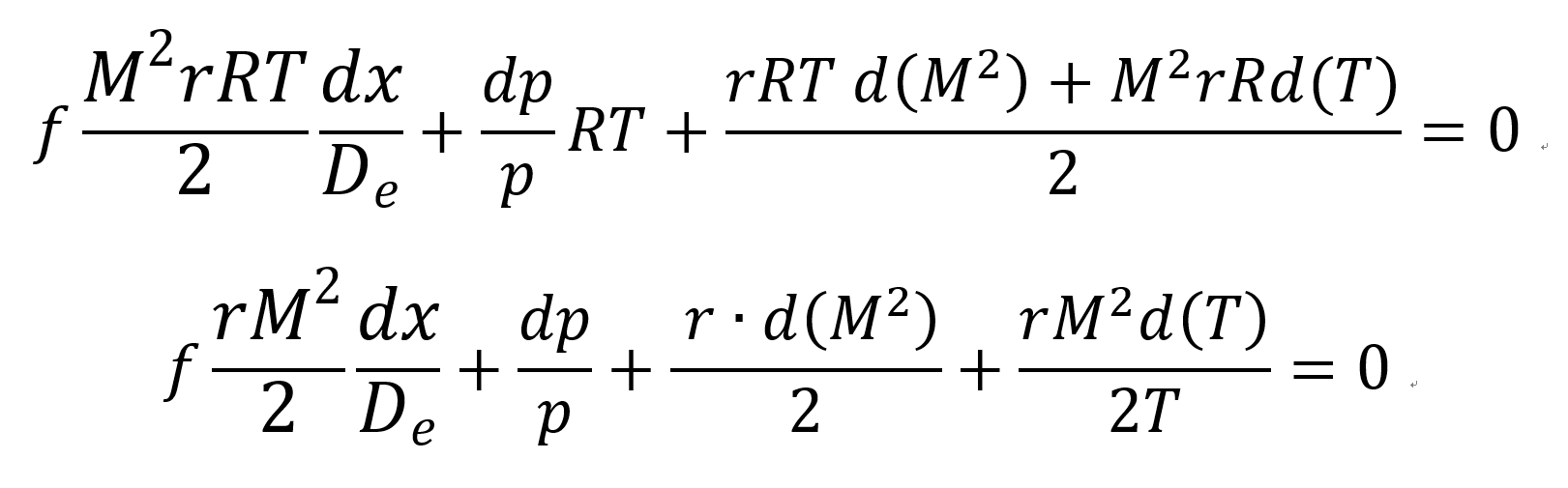
이제 dp/p와 dT/T를 f(M,r)로 표현하여,
마찰 term을 M,r로 표현해보자
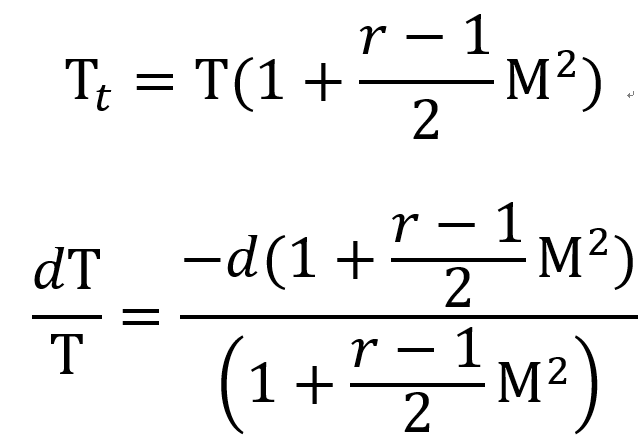

따라서 위 T,P ratio를 마찰력식에 대입해주면
정말 복잡하지만 M,r에 관한 함수로 마찰력 표현 가능..
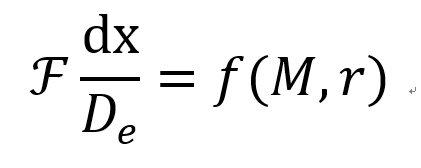
이를 State1 -> State2 로 적분해주면
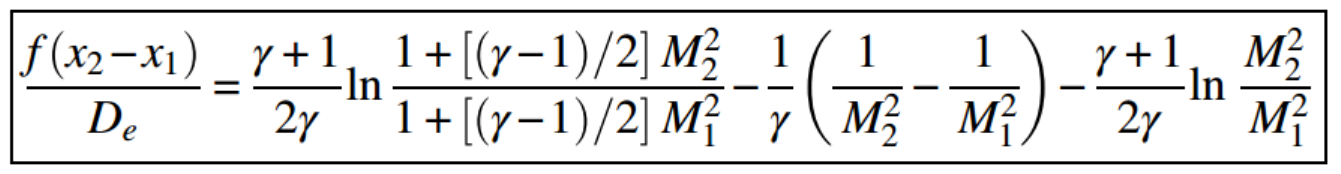
이 식이 의미하는 것은,
Friction 손실량을 우리는 M1,M2,r을 통해서 derive 할 수 있고,
Inlet M1, 관의 길이,f 를 안다면 outlet M2를 유도할 수도 있다.
여기서 과학자들은,
Expansion wave 처럼 기준점을 하나 잡아 간편한 식으로 만든후
Table에 Plot할 생각을 함.
[기준점은 다음과 같이 정의]
*: Reference point for Fanno flow 라고 부르고
기준점은 시작때 언급하였던 ds = 0 인
Fanno line에서 Ma = 1인 지점이다.
위 마찰력 식에서
State1: M1 = M, M2 = M1* = 1 을 대입해보자.
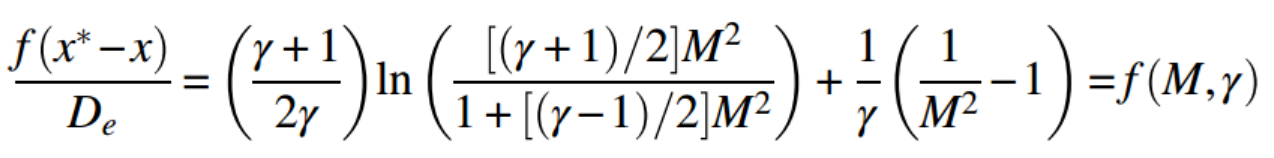
즉 우리는 Inlet Ma,r 을 알면 마찰력 term을 알 수 있다.
위 방법으로 Fanno Table에 M에 따른 f(x*-x)/D 가 표시 되어 있다.
뿐만 아니라, 조금 전에 구한 T2/T1, P2/P1, Pt2/Pt1 에도
똑같은 방법으로
State 1 - > * (reference point)
라고 생각하고
M1 = M, M2 = M* = 1 을 대입하여
M 에 따른 값들을 Fanno Table에 표시완료
잠깐.
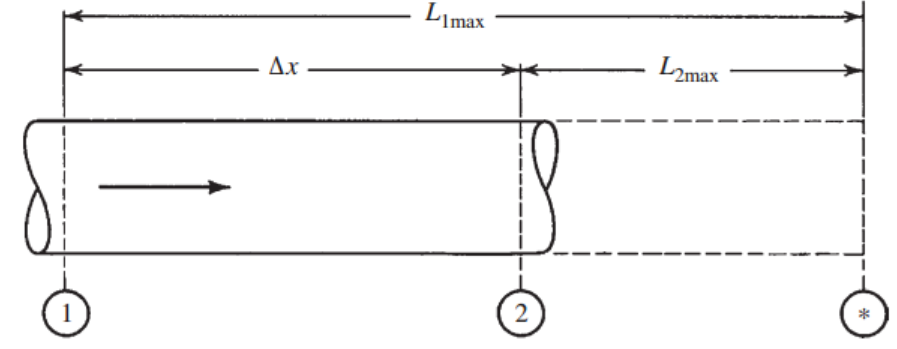
Q. 여기서 x*-x가 의마하는게 뭘까?
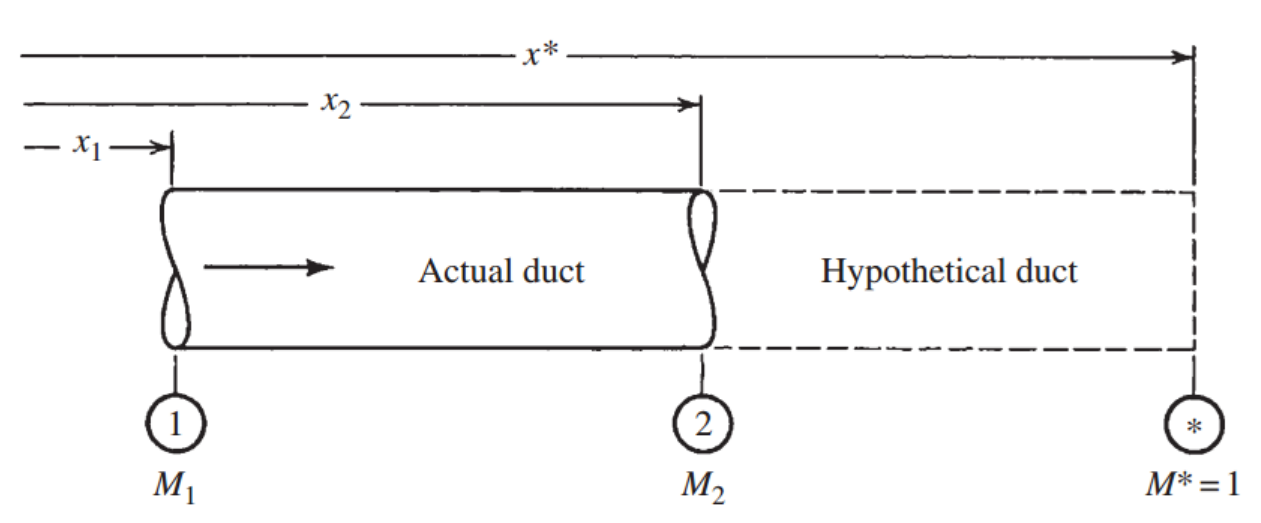
바로 Inlet Ma = M1 일때,
State 1 -> * (reference point) 까지 가기 위한
관의 길이 이다.
마지막으로 예제를 풀고 Part2로 넘어가보자.
Q. M1 = 1.80, p1 = 40psia, M2 = 1.20
find p2 and f△x/D
Fanno table을 보면,
M1 = 1.80 일때,
f(Lmax1)/D = 0.2419
= [State 1 -> * (reference point) 까지 거리]
p1/p* = 0.4741,
M2 = 1.20 일때,
f(Lmax2)/D = 0.2419
= [State 2 -> * (reference point) 까지 거리]
p2/p* = 0.8044.
따라서 State 1 -> 2거리 =
[State 1 -> * 거리] - [State 2 -> * 거리]
f△x/D = 0.2419-0.0336 = 0.208
아주 중요 별표 만개
State 2와 State1 모두 둘다 같은 Reference point를 향해서 간다
Why?

State 1 과 2 는 같은 Fanno line: ρV = G = 일정
따라서 두 State 모두 최종적으로 바라보는 지점(*)이 동일하다
결국 P1* = P2* = P*
따라서,
p2 = p2/p* x p*/p1 *p1= 0.8044 / 0.471 *40 = 67.9psia
'Gas Dynamics' 카테고리의 다른 글
| [Gas Dynamics] Ch 10 Rayleigh Flow - part 1 (2) | 2024.03.27 |
|---|---|
| [Gas Dynamics] Ch 9 Fanno Flow - part 2 - with shock (0) | 2024.03.27 |
| [Gas Dynamics] Ch 8 Prandtl-Meyer Flow - Application - Airfoil (0) | 2024.03.27 |
| [Gas Dynamics] Ch 8 Prandtl-Meyer Flow - Application - Nozzle (2) | 2024.03.26 |
| [Gas Dynamics] Ch 8 Prandtl-Meyer Flow - Expansion Flow (0) | 2024.03.26 |



