Gas Dynamics에서 우리는 Compressible flow
밀도 변화가 있는 경우 유체의 흐름을 분석하고있다.
그리고 Compressible Flow에서 가장 중요한 3가지 Factor에 대해서
Ch5에서 언급하였다
1. Area change
2. Friction
3. Heat transfer
ch 5 - Area change
ch 9 - friction Fanno flow
에 대해서 이미 앞에 두가지 요소는 다루었다.
이제는 마지막 3번째 Heat transfer이 있는 경우의 유동
Rayliegh Flow를 해석해보자
#Assumptions
1. Steady 1-D process
2. No shaft work
3. Neglect potential
4. No friction
5. Area constant
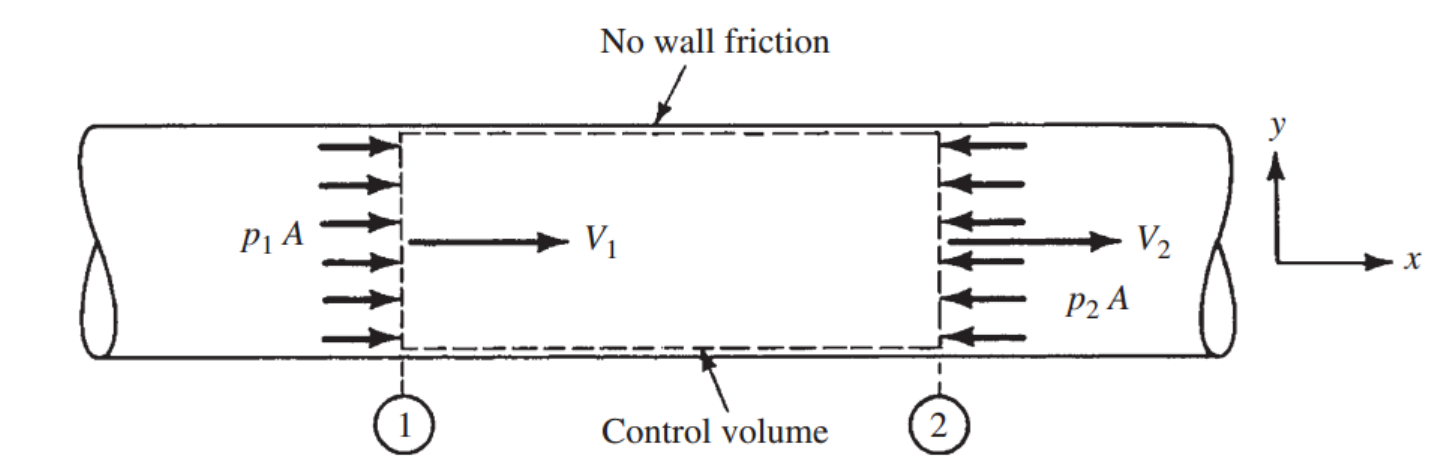
#Continuity Eq.
ρV = G = 일정
#Momentum Eq.

즉, p와 v는 G가 일정할때, 기울기가 음수인 직선함수
이제 Fanno line처럼 G가 일정할때 그래프를 Plot해보자

#Temperature line(dT = 0)
Ideal gas 식을 통해서 T가 일정할때, p와 v는 반비례함수.
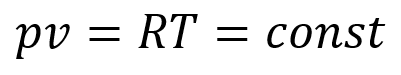
하지만, 이 그래프만 으로는 Flow 방향을 알지 못한다.
따라서 엔트로피가 증가하는 방향을 찾으러
s constant line을 그려보자
#Entropy line(ds = 0)
Ideal gas 에서 Isentropic process 일때,
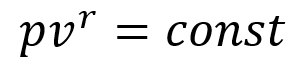
위 식을 미분해주면, 기울기를 알 수 있어 더 자세하게 Plot가능.

이제 Entropy line도 plot해보면

위 그래프를 보고 주목할 만한 사실은 2가지.
1. Flow는 1->2->3(Max T) -> 4(Max s)
에서 더이상 v가 커지지 않는다는 말.
2.T max 와 S max 차이
이를 해석하기 위해서는 엔트로피 개념을 한번 다시 짚고 가자.
[Ch2]에서 언급하였지만, 엔트로피는
Se: Reversible,
Si: Irreversilbe
두가지로 나눌 수 있다.
하지만 Assumption에서 No friction 이라고 했으므로 Si = 0
총 엔트로피 = Se term 만 존재한다.
그런데 이 reversible 엔트로피는 heat trasnfer양을 의미한다.
따라서 Heat이 들어오면 엔트로피는 증가한다는 의미이다.

However,
그래프를 다시 봐보면
State 3 -> 4 에서 엔트로피는 증가한다.
따라서 열이 계속 C.V에 들어온다는 의미이다.
그럼에도 불구하고 온도는 감소함을 알 수 있다.
이제 h-s그래프로 다시 한번 살펴보자

Fanno line과 마찬가지로
State 4 일때 ds =0, s max로 Limiting point이다.
그때,
위에서 구한 G= ρV = 일정할때,
Momentum Eq을 미분해주면
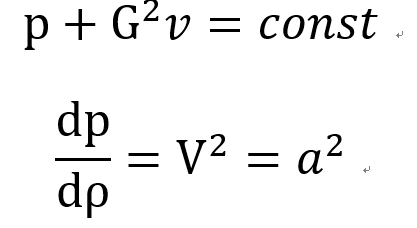
dp/dρ 는 s 일정할때 a^2 이므로
우리는 Rayliegh flow Limiting point도 Ma = 1임을 알 수 있다.
뿐만아니라,
Continuity Eq을 방금 구한 식에 대입하면.
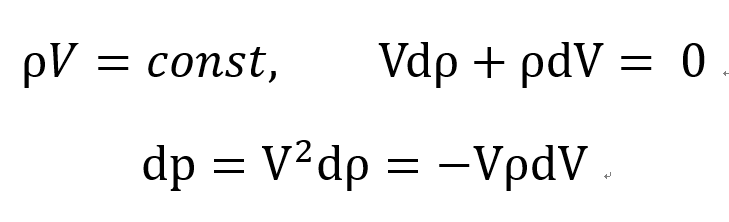
그리고 Energy eq에 위의 dp를 대입하면

Limiting point에서 Stagnatio Enthalpy는 max임을 알 수 있다.
게다가 h-s graph, Stagnation Enthalpy 기울기는 온도임을 알 수 있다.
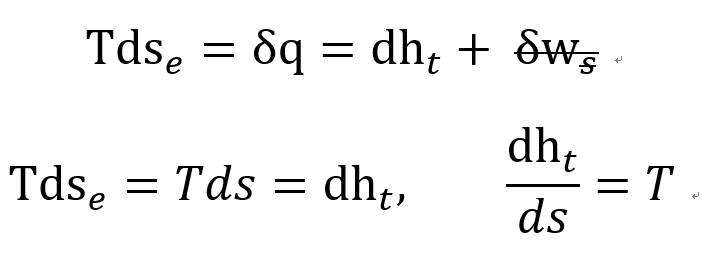
이제 State 1 -> State2 일때, Property비율들을 모두
M,r로 똑같이 표현해보자
why? 기준점잡고, Table만들려고
#압력비율 by Momentum Eq.
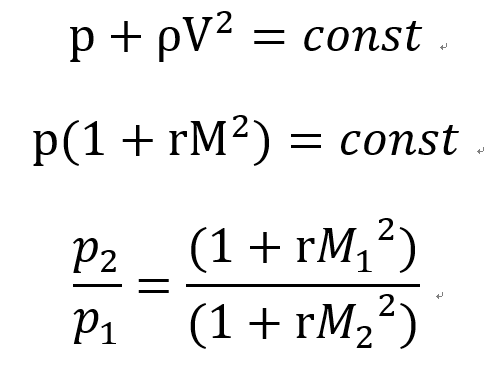
#온도비율 by Continuity Eq.
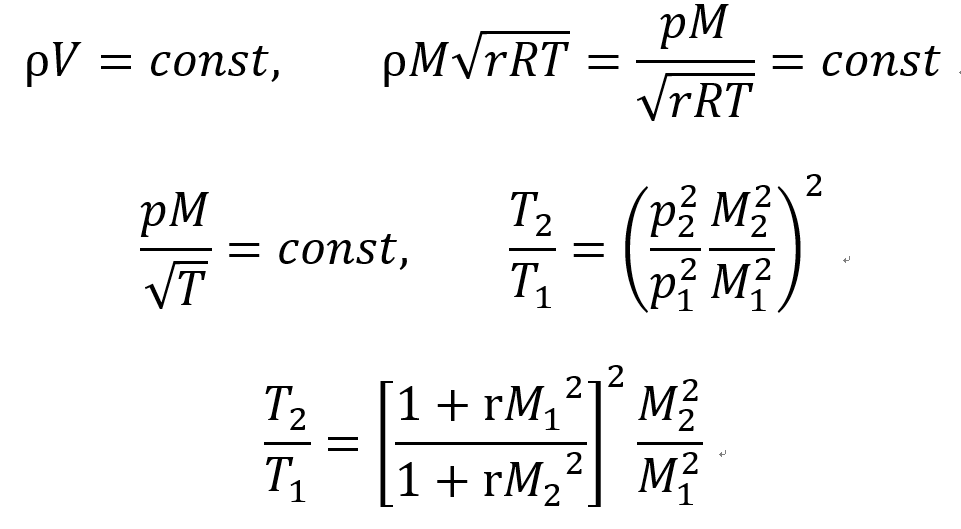
#Stagnation Temperature 비율
by static-stagnation 식 ch3
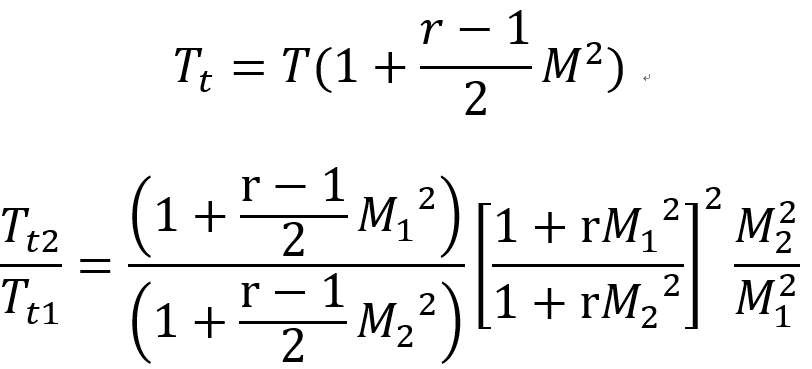
#Stagnation pressure 비율
by static-stagnation 식 ch3
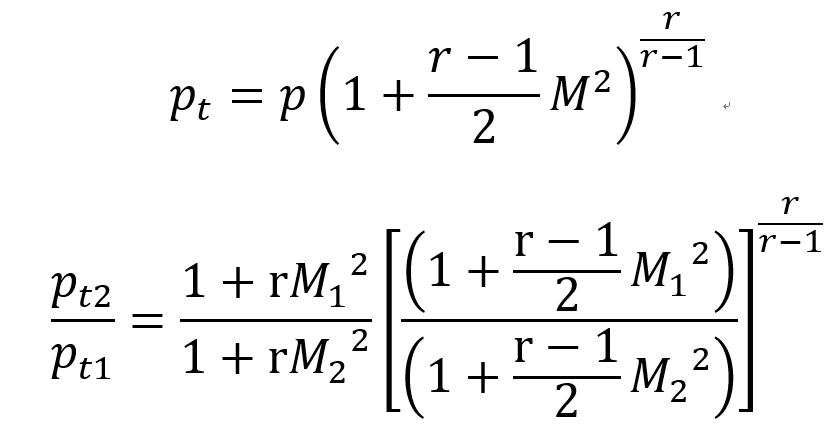
이렇게 식을 어렵게 세운 이유가 뭐다?? 기준점을 잡고, Table에 plot하려고
이제 기준점을 잡아보자
Fanno 랑 똑같이,
기준점은 Limiting point =
* reference point for Rayleigh flow
이때, Ma* = 1, ds =0, dht = 0 , s,ht 둘다 max
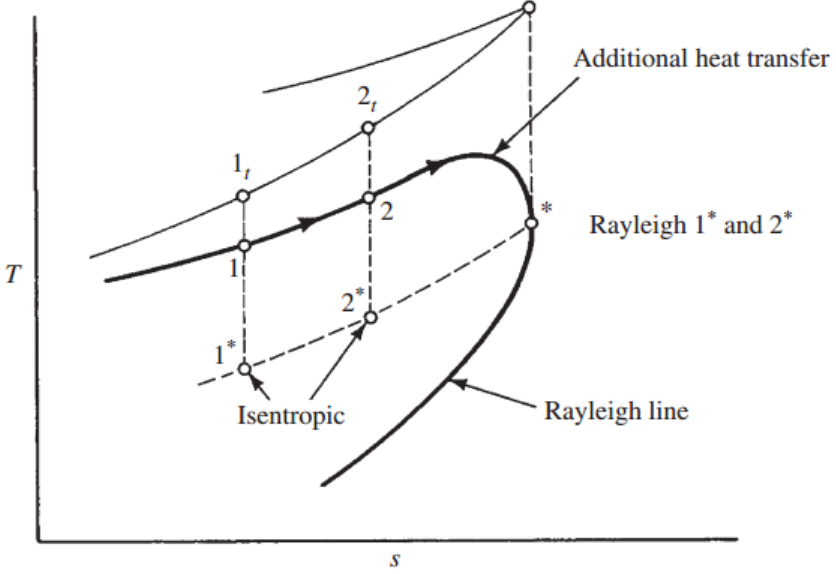
따라서 위에 구해준 식들에다가
State 1: M1 -> M
State 2: M2 -> M* =1 을 대입해주면


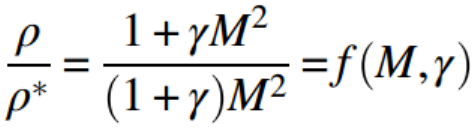
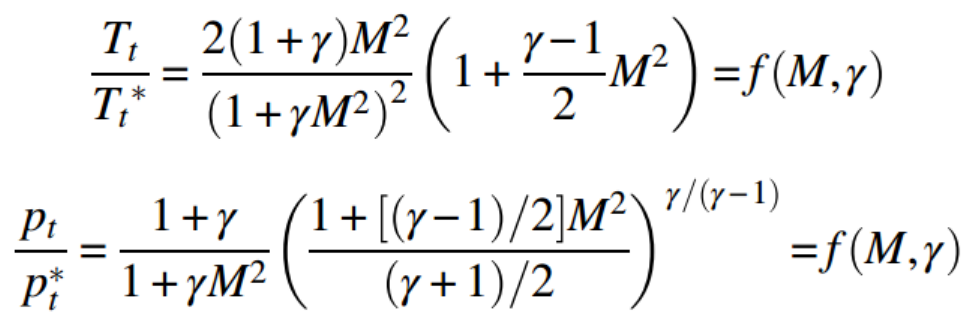
M에 따른 위 값들을 전부 Rayleigh Table에 Plot해 놓았다.
외우면 바보다.
State1 -> State2 에서
우리의 관심사중 하나는 들어온 총 열량 일것,
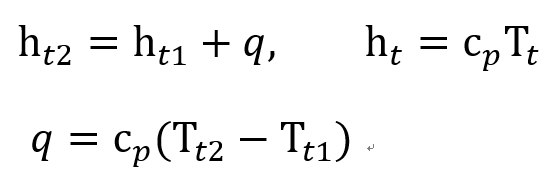
따라서, Stagnation Enthalpy 변화량을 통해서 알 수 있다.
마지막으로
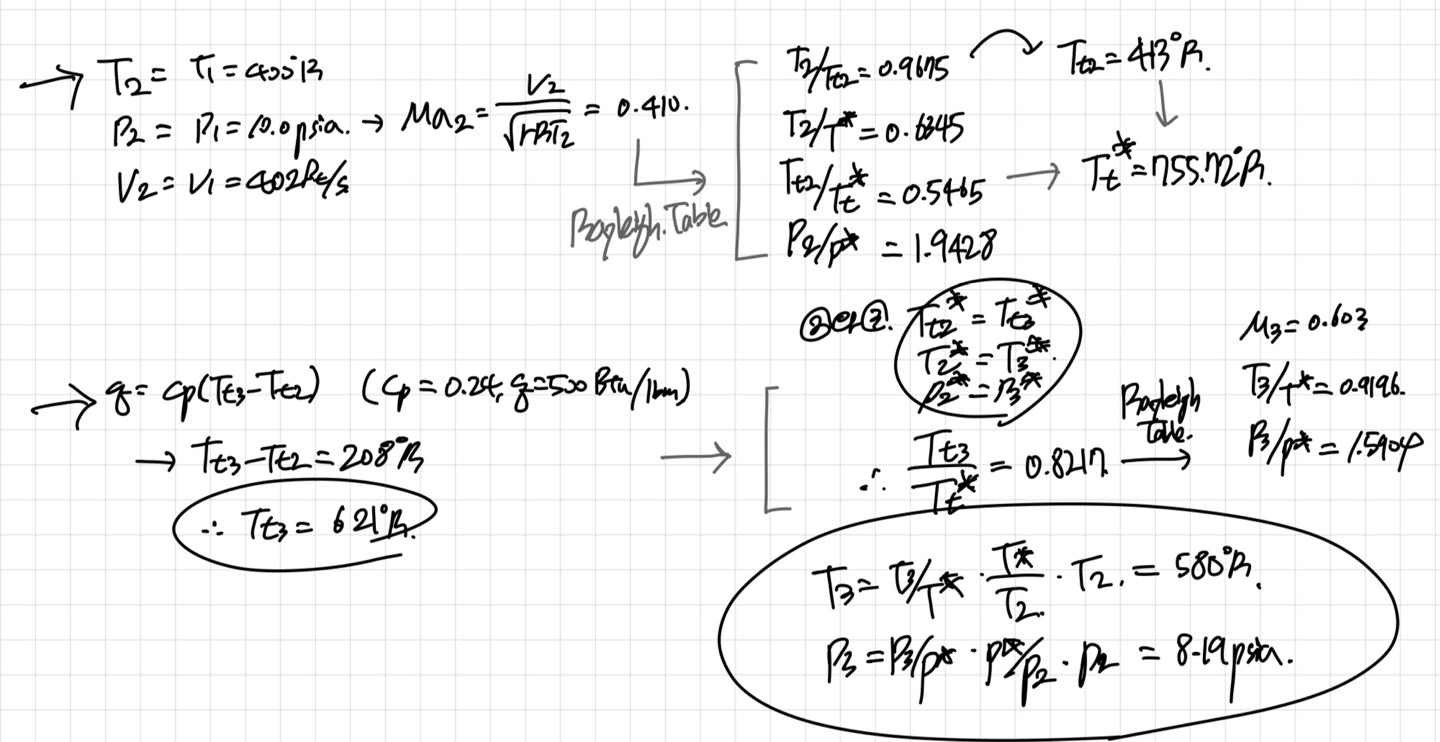
예시문제 하나를 보면서 감을 잡아보자.

'Gas Dynamics' 카테고리의 다른 글
| [Gas Dynamics] Ch 10 Rayleigh Flow - part 2 - shock and Heat chocking (0) | 2024.03.27 |
|---|---|
| [Gas Dynamics] Ch 9 Fanno Flow - part 2 - with shock (0) | 2024.03.27 |
| [Gas Dynamics] Ch 9 Fanno Flow - part 1 (0) | 2024.03.27 |
| [Gas Dynamics] Ch 8 Prandtl-Meyer Flow - Application - Airfoil (0) | 2024.03.27 |
| [Gas Dynamics] Ch 8 Prandtl-Meyer Flow - Application - Nozzle (2) | 2024.03.26 |



