일단 공학수학의 시작은 당연히 Differential equation입니다.
도대체 왜 우리는 미분을 알아야할까요?
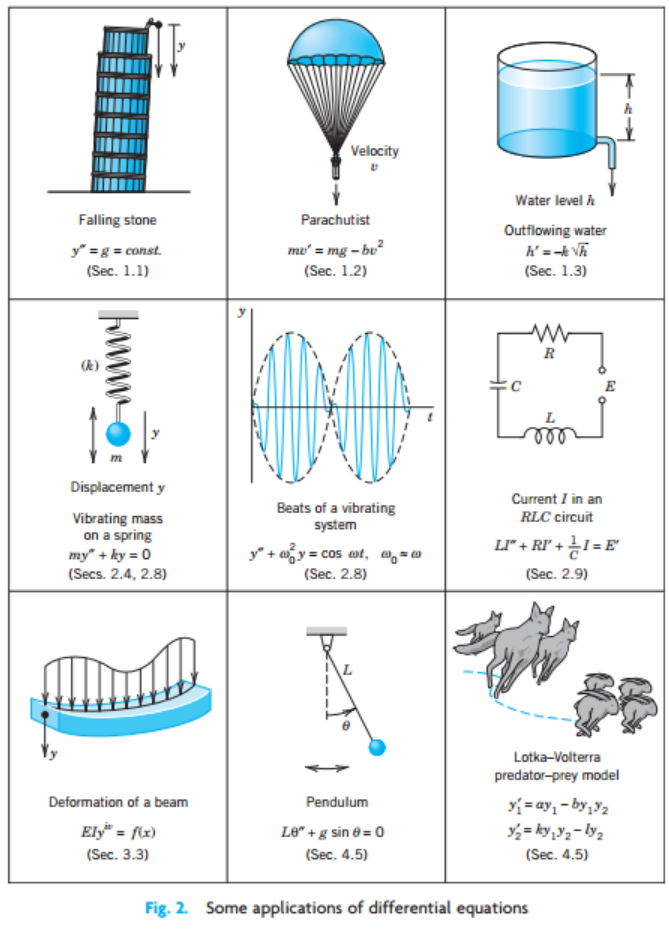
위 figure처럼 모든 자연현상들이 미분 방정식으로 표현할 수 있고,
우리는 Answer(solution)을 구함으로써 미래를 예측할 수 있기 때문이죠.
인간은 미래를 예측하고자 하고, 사고를 방지하며, 앞으로 나아가려고한다.
진격의 거인 조사병단처럼, 그냥 벽에만 있는 것을 만족못하는 거죠;;
-----------------------------------------------------------------------
여기서 가장 기본적인
Ordinary Differential Equation(ODE)
부터 시작.
ODE란???
간단하게, y=y(x)즉 x로 표현할 수 있다고 가정했을때,
y의 1차 미분, 2차 미분, 3차미분...등등등으로 구성된 함수이죠.
이렇게,
g(y, y',y'',y''', ....,x) = 0
여기서 가장 큰 미분계수를 바로 Order 이라고 정의합니다.
그렇다면, 예측해보죠
First order은 바로??
g(x,y,y') = 0 즉, y'까지 밖에 없는 함수 이겠죠????
---------------------------------------------------------------
ODE와 반대인 녀석은 바로 PDE입니다.
편미분 (Partial derivative) 가 포함되어있는 미분 방정식이죠.
나중 챕터에서 자세하게 다루겠지만, 편미분이 뭔지부터???? 생각해보죠
자 u=u(x,y)즉 x,y두개의 변수로 구성되었다고 생각해봅시다.
여기서 질문 u를 x로 미분하세요 하면? 어떻게 하시겠어요??
그냥 단순하게 du/dx?????
이러면 문제가 생깁니다 왜??? y=y(x)즉 y도 x에 따라서 변하기 때문이죠.
그래서 우리는 편미분이라는 것을 사용합니다.
편미분은 du(x,y)/dx에서 "y를 상수로 취급하고 진짜 x만 미분해줘" 라는 것입니다!
그리고 기호는 다음과 같이 표현합니다

---------------------------------------------------------------
What we gonna do???
항상 공부를 할때, 흐름을 놓치고는 합니다. 저도 항상 내가 뭐하고있는거지?
[그니까 이걸 왜 배우지를 순서대로 ㄱ ㅖ속 remind해야만 함..]
그렇다면 우리가 1st ODE로부터 하고싶은게 뭐야? 뭘하면 되는거야 라고했을떄?
바로 g(x,y,y') =0 이라는 식으로부터,
y = h(x) 로 표현 하는게 바로 최종목표
그리고 이 h(x)를 Solution 이라고 부릅니다.
하지만, 모든 Solution은 적분을 통해서 derived 되기 때문에 상수가 무조건 있다는것.
결국, 상수가 있는 solution은 Genearal Solution
Inital value y0=h(x0)를 대입해줘서 상수를 없앤 solution은 particular solution이라고 합니다.
---------------------------------------------------------------
여기서 그냥 일반적인 1st order ODE를 푸는 공식은 없습니다.
우리가 할 수 있는 것은, ODE의 종류를 나누고, 각 종류에서의 해를 구하는 것 만 가능;;;
1. Separable ODE
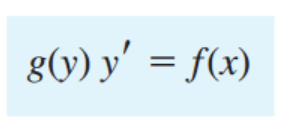
단순하게, 왼쪽은 y만 오른쪽은 x로 separate 할 수 있다면??? 우리는 Separable ODE라고 부르고,
해는 단순하게 그냥 양쪽을 적분.
너무 쉽죠. (y'=dy/dx 라는것 잊지말아야죠)
[General solution]
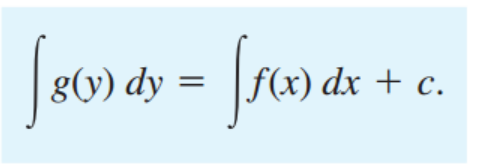
사실 이렇게 간단하게 보통 ODE는 없겠죠?? 그니까 책이 두껍겠죠..
여기서 바로 강제로 separable form 으로 만들어주는 방법이 있습니다.
[Extended Method: Reduction to Separable Form]
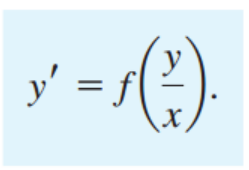
u=y/x 라 치환해주면, y=ux, y'=u'x+u
정리해주면, u'x+u = f(u), u'x = f(u)-u
여기서 u'=du/dx임을 이용하여 왼쪽은 u 오른쪽은 x에 관한 식으로 만들어주면 Separable 완성
1/(f(u)-u) du = xdx/x
2. Exact ODE
1stODE에서 가장 중요한 Exact ODE. 순서를 잘 이해하셔야 됩니다!
시작은 바로, Chain rule
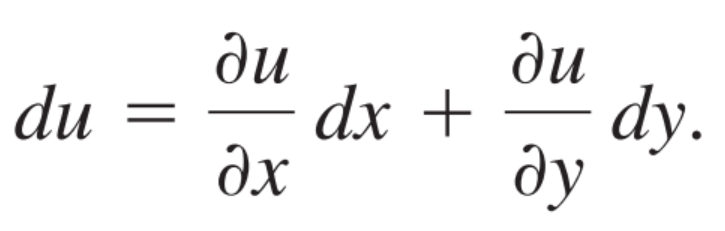
만약에, u(x,y) = constant인 식이 존재한다면, 위식 du = 0
그리고, 우리는 다음과 같은 1st ODE가 있다고 하자, 그리고 M,N을 각각 u의 x,y 편미분으로 정의 하자.
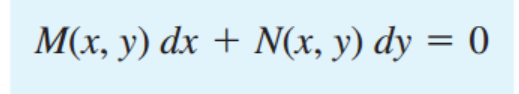

M,N을 각각 y,x,로 한번더 편미분해주자 신기하게 결과 값이 같은 것을 알 수 있다.
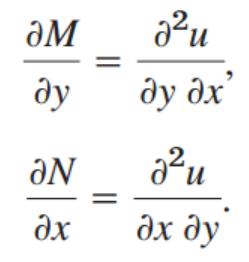
따라서,
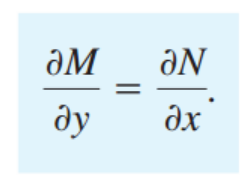
결론적으로, 1stODE에서 식(a)와 (b)를 적분해주면. Generatl solution u 를 도출 할 수 있다.
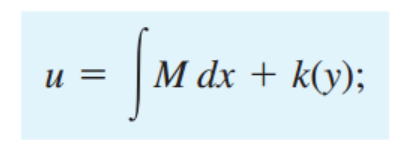
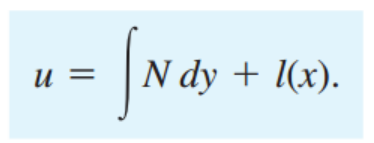
--------------------------------------------------------------
그니까, 순서를 잘 기억 해야한다. 만약에 만약에 밑의 형태의 1stODE가 있다면, 의심해 봐야된다. 이게 Exact ODE일까??
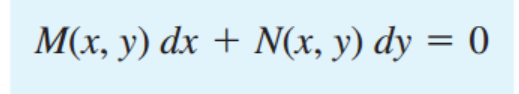
확인 방법은. 밑의 식이 성립하는지 안하는지, 성립한다면
-> M(x,y) = u의 x편미분, N(x,y) = u의 y편미분이라는 말이다. 그 말은 즉,
u(x,y) = constant, du = 0이라는 말이므로!!!!!!!! u를 M,N의 적분꼴로 도출 할 수있다는 말!
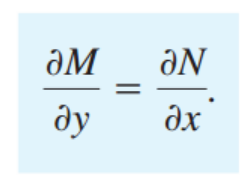
예제로 감을 잡아보고 다음 poster에서 이어서~

'Advanced Engineering Mathematics' 카테고리의 다른 글
| [Engineering Mathematics] Ch 3. Higher-order Linear ODE (0) | 2024.04.09 |
|---|---|
| [Engineering Mathematics] Ch 2. 2st-order ODE - part 3 (0) | 2024.04.09 |
| [Engineering Mathematics] Ch 2. 2st-order ODE - part 2 (0) | 2024.04.09 |
| [Engineering Mathematics] Ch 2. 2st-order ODE - part 1 (0) | 2024.04.09 |
| [Engineering Mathematics] Ch 1. 1st-order ODE - part 2 (0) | 2024.04.09 |



