Ch1에서는 1st order ODE를 다뤘습니다.
이제는 다음 단계 2차로 넘어가보죠.
2nd order linear ODE는
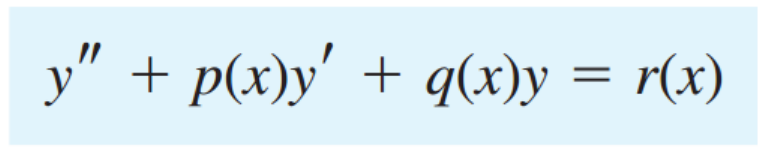
다음과 같이 표현되고 Homogenous는 r(x) =0, non-Homogenous 는 r(x) nonzero 인경우.
우리가 하고싶은 것은 ? y=f(x)를 찾는것!
일단 Homogenous Linear ODE부터 어떻게 해를 구하는지 살혀보죠.\
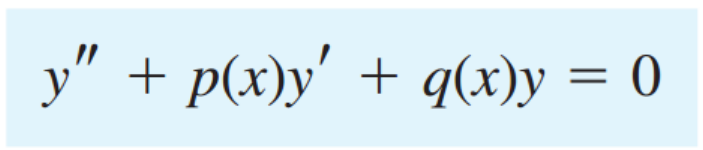
여기서 중요한 개념부터 알고 들어갑십다.
1.Superpositon principle
2. Linearity pinciple
1. Superposition
사실 정말 간단합니다. 위 방정식의 해 y1,y2 두개를 구했다고 해보죠.
그렇다면??
y1'' +py1' + qy1 =0
y2'' + py2' + qy2 = 0
이겠죠??
두식을 더하면
(y1+y2)'' + p(y1+y2)' + q(y1+y2) =0
즉,,, y1+y2 도 해가 된다는 것입니다. 이게 바로 Superposition principle
"해들의 합은 사실 해이다"
2. Linearity
이것도 사실 간단합니다. 어떤 해 y1이 있다고 했을때,
ay1도( a는 임의의 상수)도 해가 된다는 것이죠.
방정식에 대입해보면 상식적이게 됩니다.
이 상식적인 위 principle이 나중에 쓰인다는것!
Initial Value Problem
거의 모든 2nd order ODE는 두개의 Inital value가 주어집니다.

위 두개의 조건을 만족하기 위해서, General Soltuion은
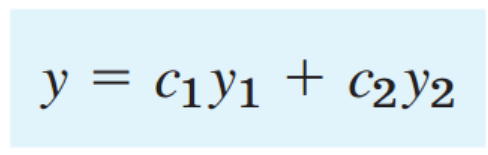
위처럼 두개의 해의 합과 상수로 표현 됩니다!
그러면 여기서 의문점이 생기죠?? 왜꼭 두개인가?
두개 이어야 하는 이유?
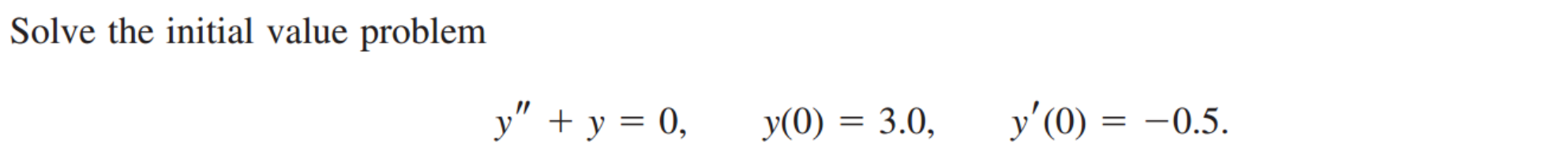
위 문제의 경우, y = c1 cosx 가 해임을 대입을 통해서 알 수 있습니다.
만약에 이게 유일한 해라면??, initial value를 대입해보면,
3 = c1, -0.5 = 0 이라는 불가능한 답이 나옵니다.
따라서, inital value가 두개인 이상, General soltution은 두개의 해의 합으로 표현 됩니다.
위의 연장선으로, y1과 y2가 서로 비례하는 즉, y1=u y2(u는 상수) 라면,
결국 y = c1y1+c2y2 = C * y1 이 되죠.
그 말은 불가능하다는 이야기입니다.
따라서, y1과 y2는 비례관계이면 절대 안된다는 것입니다.
이것을 수학적으로 표현 한 문장이 바로.

이고, y1과 y2는 Linearly independent하다 라고 말합니다.
우리는 linearly independent한 두해 y1,y2를 basis of solution 이라고 정의
-----------------------------------------------------------------------------
만약에 y1,y2중 한개 y1만 알경우, 우리는 위 원리대로 y2를 구할 수 있습니다.
이것을 Redcution of Order
증명) 밑 식의 해 y1을 안다고 가정하고, y2를 구해봅시다.

y2 = u(x) y1이라고 정의하고 대입하게 되면,

마지막 식에서 오른쪽은 0 이고, u' = U, u'' = U' 이라고 정의하면, 1st Order ODE식으로 바뀌게 됩니다.
결국 2nd ODE -> 1st ODE 로 바꾸어서 Reduction of order method라고 부른것.

따라서, 최종 해는

'Advanced Engineering Mathematics' 카테고리의 다른 글
| [Engineering Mathematics] Ch 3. Higher-order Linear ODE (0) | 2024.04.09 |
|---|---|
| [Engineering Mathematics] Ch 2. 2st-order ODE - part 3 (0) | 2024.04.09 |
| [Engineering Mathematics] Ch 2. 2st-order ODE - part 2 (0) | 2024.04.09 |
| [Engineering Mathematics] Ch 1. 1st-order ODE - part 2 (0) | 2024.04.09 |
| [Engineering Mathematics] Ch 1. 1st-order ODE. (0) | 2024.04.08 |



